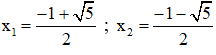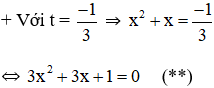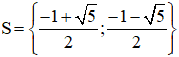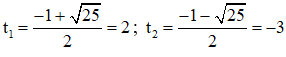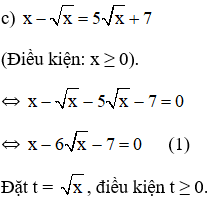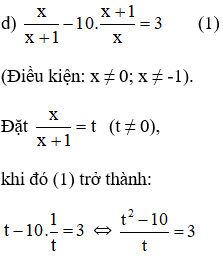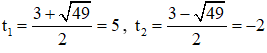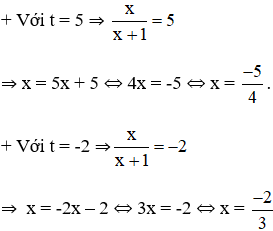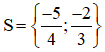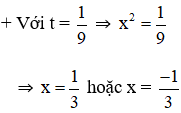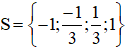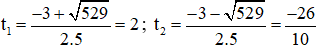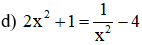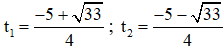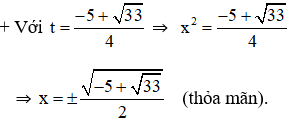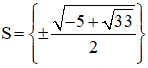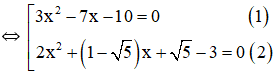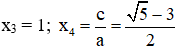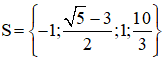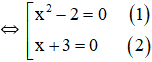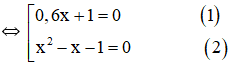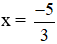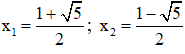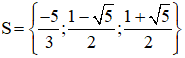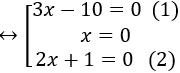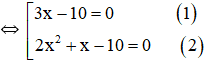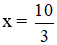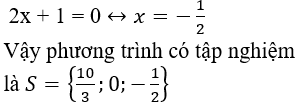Giải phương trình bằng cách đặt ẩn phụ:

$\begin{array}{l}a)3.{\left(x^2+x\right)}^2-2\left(x^2+x\right)-1=0\\ b){\left(x^2-4x+2\right)}^2+x^2-4x-4=0\\ c)x-\sqrt{x}=5\sqrt{x}+7\\ d)\frac{x}{x+1}-10\cdot \frac{x+1}{x}=3\end{array}$

$\text{ a) }9x^4-10x^2+1=0\left(1\right)$

Đặt $x^2=t$, điều kiện t ≥ 0.

Khi đó (1) trở thành : $9t^2-10t+1=0\left(2\right)$

Giải (2):

Có a = 9 ; b = -10 ; c = 1

⇒ a + b + c = 0

⇒ Phương trình (2) có nghiệm ${\mathrm{t}}_1=1;{\mathrm{t}}_2=\mathrm{c}/\mathrm{a}=1/9$

Cả hai nghiệm đều thỏa mãn điều kiện.

+ Với t = 1 $\Rightarrow x^2=1$ ⇒ x = 1 hoặc x = -1.

Vậy phương trình (1) có tập nghiệm 

b)

$\begin{array}{l}5x^4+2x^2-16=10-x^2\\ \iff 5x^4+2x^2-16-10+x^2=0\\ \iff 5x^4+3x^2-26=0\end{array}$

Đặt $x2 = t$, điều kiện t ≥ 0.

Khi đó (1) trở thành : $5t^2+3t-26=0\left(2\right)$

Giải (2) :

Có a = 5 ; b = 3 ; c = -26

$\Rightarrow \Delta =3^2-4.5\cdot (-26)=529>0$

⇒ Phương trình có hai nghiệm phân biệt

Đối chiếu điều kiện chỉ có $t1 = 2$ thỏa mãn

+ Với t = 2 ⇒ $\Rightarrow x^2=2$ ⇒ x = √2 hoặc x = -√2.

Vậy phương trình (1) có tập nghiệm S = {-√2; √2}

c) $0,3x^4+1,8x^2+1,5=0\left(1\right)$

Đặt  $x^2=t$, điều kiện t ≥ 0.

Khi đó, (1) trở thành : $0,3t^2+1,8t+1,5=0\left(2\right)$

Giải (2) :

có a = 0,3 ; b = 1,8 ; c = 1,5

⇒ a – b + c = 0

⇒ Phương trình có hai nghiệm ${\text{t}}_1=-1{\text{ và t}}_2=-\text{c}/\text{a}=-5$

Cả hai nghiệm đều không thỏa mãn điều kiện.

Vậy phương trình (1) vô nghiệm.

Điều kiện xác định: x ≠ 0.

Quy đồng, khử mẫu ta được :

$\begin{array}{l}2x^4+x^2=1-4x^2\\ \iff 2x^4+x^2+4x^2-1=0\\ \iff 2x^4+5x^2-1=0\left(1\right)\end{array}$

Đặt $t=x^2$, điều kiện t > 0.

Khi đó (1) trở thành : $2t^2+5t-1=0\left(2\right)$

Giải (2) :

Có a = 2 ; b = 5 ; c = -1

$\Rightarrow \Delta =5^2-4.2\cdot (-1)=33>0$

⇒ Phương trình có hai nghiệm phân biệt:

Đối chiếu với điều kiện thấy có nghiệm $t1$ thỏa mãn.

Vậy phương trình có tập nghiệm 

a) $\left(3x^2-7x-10\right)\cdot \left[2x^2+(1-5)x+5-3\right]=0$

+ Giải (1):

$3x^2 – 7x – 10 = 0$

Có a = 3; b = -7; c = -10

⇒ a – b + c = 0

⇒ (1) có hai nghiệm $x_1 = -1 và x_2 = -c/a = 10/3.$

+ Giải (2):

$2x^2 + (1 - \surd 5)x + \surd 5 - 3 = 0$

Có a = 2; b = 1 - √5; c = √5 - 3

⇒ a + b + c = 0

⇒ (2) có hai nghiệm:

Vậy phương trình có tập nghiệm 

b)

$\begin{array}{l}{x}^3+3x^2-2x-6=0\\ \iff \left(x^3+3x^2\right)-(2x+6)=0\\ \iff x^2(x+3)-2(x+3)=0\\ \iff \left(x^2-2\right)(x+3)=0\end{array}$

+ Giải (1): $x^2 – 2 = 0 \iff x^2 = 2$ ⇔ x = √2 hoặc x = -√2.

+ Giải (2): x + 3 = 0 ⇔ x = -3.

Vậy phương trình có tập nghiệm S = {-3; -√2; √2}

c)

$\begin{array}{l}\left(x^2-1\right)(0,6x+1)=0,6x^2+x\\ \iff \left(x^2-1\right)(0,6x+1)=x\cdot (0,6x+1)\\ \iff \left(x^2-1\right)(0,6x+1)-x(0,6x+1)=0\\ \iff (0,6x+1)\left(x^2-1-x\right)=0\end{array}$

+ Giải (1): 0,6x + 1 = 0 ⇔ 

+ Giải (2):

$x^2 – x – 1 = 0$

Có a = 1; b = -1; c = -1

$\Rightarrow \Delta = {(-1)}^2 – 4.1.(-1) = 5 > 0$

⇒ (2) có hai nghiệm 

Vậy phương trình có tập nghiệm 

d)

$\begin{array}{l}{\left(x^2+2x-5\right)}^2={\left(x^2-x+5\right)}^2\\ \iff {\left(x^2+2x-5\right)}^2-{\left(x^2-x+5\right)}^2=0\\ \iff \left[\left(x^2+2x-5\right)-\left(x^2-x+5\right)\right]\cdot \left[\left(x^2+2x-5\right)+\left(x^2-x+5\right)\right]=0\\ \iff (3x-10)\left(2x^2+x\right)=0\end{array}$

⇔ (3x-10).x.(2x+1)=0

+ Giải (1): 3x – 10 = 0 ⇔ 

+ Giải (2):