Câu hỏi:
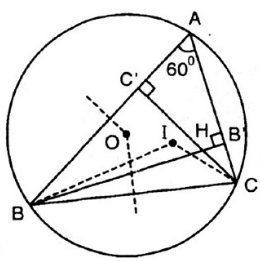
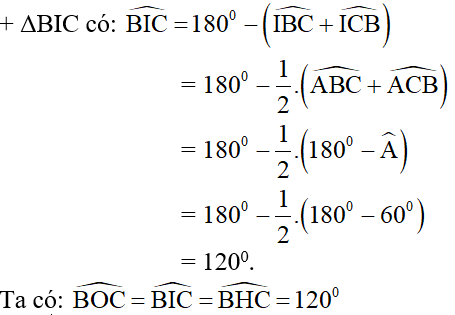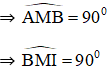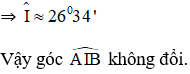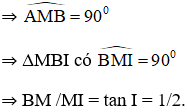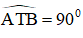12/07/2024 2,353Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác ABC với . Gọi H là giao điểm của các đường cao BB'và CC'.
Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.
Quảng cáo
Trả lời:
Giải bởi Vietjack
⇒ B, O, I, H, C cùng thuộc đường tròn chứa cung 120º dựng trên đoạn BC.
Kiến thức áp dụng
+ Các điểm cùng nhìn một đoạn thẳng cố định dưới cùng một góc α thì đều thuộc cùng một đường tròn.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
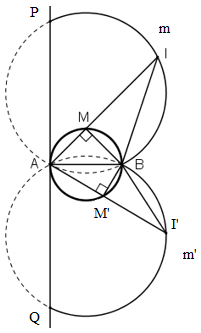
a) M ∈ đường tròn đường kính AB
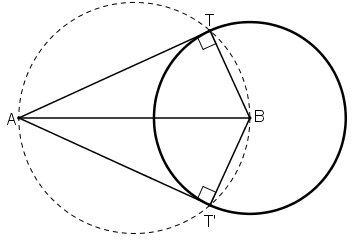
ΔBMI vuông tại M
⇒ tan I = MB / MI = 1/2
b) Dự đoán: Quỹ tích điểm I là hai cung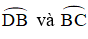 
là các cung chứa góc 26º34’ dựng trên đoạn AB.
Chứng minh:
+ Phần thuận :
Theo phần a):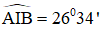 
không đổi
I nằm trên cung chứa góc 26º34’ dựng trên đoạn AB cố định
Kẻ tiếp tuyến của đường tròn tại A cắt hai cung chứa góc 26º34’ dựng trên đoạn AB tại C và D
Khi M di động trên đường tròn đường kính AB cố định thì I di động trên cung BC và BD
⇒ I nằm trên hai cung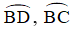 
chứa góc 26º34’ dựng trên đoạn AB cố định.
+ Phần đảo:
Lấy điểm I bất kỳ nằm trên hai cung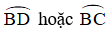 
nhìn AB dưới 1 góc 26º34’.
AI cắt đường tròn đường kính AB tại M.
⇒ BM /MI = tan I = 1/2.
Kết luận: Quỹ tích điểm I là hai cung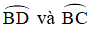 
nhìn AB dưới góc 26º34’ (hình vẽ).
Kiến thức áp dụng
+ Trong một tam giác vuông, tan α = cạnh đối / cạnh huyền.
Lời giải
Dự đoán: Quỹ tích là đường tròn đường kính AB.
Chứng minh:
+ Phần thuận:
AT là tiếp tuyến của đường tròn tâm B
⇒ AT ⊥ BT
⇒ 
⇒ T thuộc đường tròn đường kính AB.
+ Phần đảo:
Lấy T thuộc đường tròn đường kính AB
⇒
⇒ AT ⊥ TB và BT < AB
⇒ AT tiếp xúc với đường tròn tâm B, bán kính BT < BA.
Kết luận: Quỹ tích các tiếp điểm là đường tròn đường kính AB.
Kiến thức áp dụng
+ Thông thường, bài toán quỹ tích ta làm theo các bước:
1, Dự đoán quỹ tích
2, Chứng minh quỹ tích: gồm Phần thuận và Phần đảo
3, Kết luận.
+ Quỹ tích các điểm nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 1. Phương trình quy về phương trình bậc nhất một ẩn có đáp án
Nhắn tin Zalo