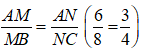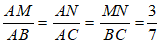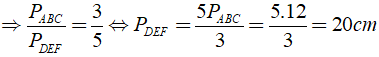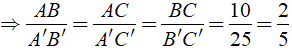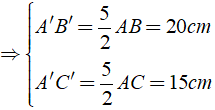Câu hỏi:

31/08/2020 502

Cho tam giác ABC, trên đoạn thẳng AB và AC lấy các điểm M và N sao cho AM = 6cm; MB = 8cm; AN = 3cm và AC = 7cm. Tìm khẳng định sai ?

A. MN/BC = 3/7

B. Hai tam giác AMN và ABC đồng dạng với nhau

C. MN// BC

D. Tam giác AMC đồng dạng với tam giác ABN.

Xem lời giải

Câu hỏi trong đề: Bài tập Khái niệm hai tam giác đồng dạng (có lời giải chi tiết) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có: NC = AC – AN = 7 – 3 = 4cm

Vì

Bài tập: Khái niệm hai tam giác đồng dạng | Lý thuyết và Bài tập Toán 8 có đáp án

nên MN // BC (định lí Ta let đảo)

Suy ra: Tam giác AMN đồng dạng với tam giác ABC.

Ta có:

Bài tập: Khái niệm hai tam giác đồng dạng | Lý thuyết và Bài tập Toán 8 có đáp án

Chọn đáp án D

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho Δ ABC đồng dạng Δ DEF có tỉ số đồng dạng là k = 3/5, chu vi của Δ ABC bằng 12cm. Chu vi của Δ DEF là?

A. 7,2cm

B. 20cm

C. 3cm

D. 17/3cm

Lời giải

Ta có: Δ ABC đồng dạng Δ DEF

Bài tập: Khái niệm hai tam giác đồng dạng | Lý thuyết và Bài tập Toán 8 có đáp án

Chọn đáp án B.

Câu 2

Cho Δ ABC có AB = 8cm,AC = 6cm,BC = 10cm. Tam giác A'B'C' đồng dạng với tam giác ABC có độ dài cạnh lớn nhất là 25 cm. Tính độ dài các cạnh còn lại của Δ A'B'C' ?

A. 4cm; 3cm

B. 7,5cm; 10cm

C. 4,5cm; 6cm

D. 15cm; 20cm

Lời giải

Ta có: Δ ABC đồng dạng Δ A'B'C'

Bài tập: Khái niệm hai tam giác đồng dạng | Lý thuyết và Bài tập Toán 8 có đáp án

Chọn đáp án D.

Câu 3

Cho Δ ABC đồng dạng Δ A'B'C' có AB/A'B' = 2/5. Biết hiệu số chu vi của Δ A'B'C' và Δ ABC là 30cm. Phát biểu nào sau đây đúng?

A. Chu vi của Δ ABC là 20cm, chu vi của Δ A'B'C' là 50cm.

B. Chu vi của Δ ABC là 50cm, chu vi của Δ A'B'C' là 20cm.

C. Chu vi của Δ ABC là 45cm, chu vi của Δ A'B'C' là 75cm.

D. Cả 3 đáp án đều sai.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hai tam giác ABC và MNP có:
$\frac{A B}{M N} = \frac{A C}{M P} = \frac{B C}{N P} v à \hat{A} = \hat{M}; \hat{B} = \hat{N}$
Tìm khẳng định đúng

A. Hai tam giác ABC và MNP đồng dạng với nhau.

B. Chưa thể kết luận hai tam giác này đồng dạng.

C. $∠ C \neq ∠ P$

D. Tất cả sai.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho Δ ABC đồng dạng Δ A'B'C' có AB = 3A'B'. Kết quả nào sau đây sai?

A. $\hat{A} = \hat{A'}; \hat{B} = \hat{B'}$

B. $A' C' = \frac{1}{3} A C$

C. $\frac{A C}{B C} = \frac{A' C'}{B' C'} = 3$

D. $\frac{A B}{A' B'} = \frac{A C}{A' C'} = \frac{B C}{B' C'}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho tam giác ABC, gọi M, N và P theo thứ tự là trung điểm của AB, AC và BC. Khi đó tam giác AMN đồng dạng với tam giác nào

A. ΔAMC

B. ΔABC

C. ΔABP

D. ΔAPC

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho tam giác ABC, điểm M thuộc cạnh BC sao cho $\frac{M B}{M C} = \frac{1}{2}$ . Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Biết chu vi tam giác ABC bằng 30cm. Chu vi của các tam giác DBM và EMC lần lượt là

A. 10cm; 15cm

B. 12cm; 16cm

C. 20cm; 10cm

D. 10cm; 20cm

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho tam giác ABC, trên đoạn thẳng AB và AC lấy các điểm M và N sao cho AM = 6cm; MB = 8cm; AN = 3cm và AC = 7cm. Tìm khẳng định sai ?

Bình luận

Cho Δ ABC đồng dạng Δ DEF có tỉ số đồng dạng là k = 3/5, chu vi của Δ ABC bằng 12cm. Chu vi của Δ DEF là?

Cho Δ ABC có AB = 8cm,AC = 6cm,BC = 10cm. Tam giác A'B'C' đồng dạng với tam giác ABC có độ dài cạnh lớn nhất là 25 cm. Tính độ dài các cạnh còn lại của Δ A'B'C' ?

Cho Δ ABC đồng dạng Δ A'B'C' có AB/A'B' = 2/5. Biết hiệu số chu vi của Δ A'B'C' và Δ ABC là 30cm. Phát biểu nào sau đây đúng?

Cho hai tam giác ABC và MNP có:ABMN=ACMP=BCNP và A^=M^; B^=N^Tìm khẳng định đúng

Cho Δ ABC đồng dạng Δ A'B'C' có AB = 3A'B'. Kết quả nào sau đây sai?

Cho tam giác ABC, gọi M, N và P theo thứ tự là trung điểm của AB, AC và BC. Khi đó tam giác AMN đồng dạng với tam giác nào

Cho tam giác ABC, điểm M thuộc cạnh BC sao cho MBMC=12. Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Biết chu vi tam giác ABC bằng 30cm. Chu vi của các tam giác DBM và EMC lần lượt là

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hai tam giác ABC và MNP có:
$\frac{A B}{M N} = \frac{A C}{M P} = \frac{B C}{N P} v à \hat{A} = \hat{M}; \hat{B} = \hat{N}$
Tìm khẳng định đúng