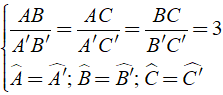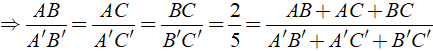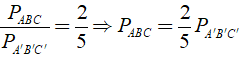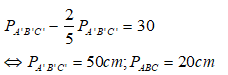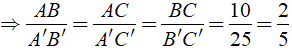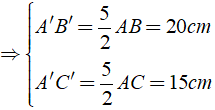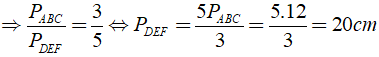Bài tập Khái niệm hai tam giác đồng dạng (có lời giải chi tiết)
50 người thi tuần này 4.6 3.4 K lượt thi 16 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 09
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 08
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 07
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Danh sách câu hỏi:
Câu 1
A. MN/AB = MP/AC
B. MN/AB = MP/BC
C. MN/AB = NP/AC
D. MN/BC = NP/AC
Lời giải
Ta có: Δ MNP đồng dạng Δ ABC ⇒ MN/AB = NP/BC = MP/AC
Chọn đáp án A.
Lời giải
Ta có: Δ ABC đồng dạng Δ A'B'C' ⇒
Đáp án C sai.
Chọn đáp án C.
Câu 3
A. Chu vi của Δ ABC là 20cm, chu vi của Δ A'B'C' là 50cm.
B. Chu vi của Δ ABC là 50cm, chu vi của Δ A'B'C' là 20cm.
C. Chu vi của Δ ABC là 45cm, chu vi của Δ A'B'C' là 75cm.
D. Cả 3 đáp án đều sai.
Lời giải
Ta có: Δ ABC đồng dạng Δ A'B'C'
Khi đó
Mà PA'B'C' - PABC = 30cm.
Suy ra
Vậy chu vi của Δ ABC là 20cm, chu vi của Δ A'B'C' là 50cm.
Chọn đáp án A.
Câu 4
A. 4cm; 3cm
B. 7,5cm; 10cm
C. 4,5cm; 6cm
D. 15cm; 20cm
Lời giải
Ta có: Δ ABC đồng dạng Δ A'B'C'
Chọn đáp án D.
Câu 5
A. 7,2cm
B. 20cm
C. 3cm
D. 17/3cm
Lời giải
Ta có: Δ ABC đồng dạng Δ DEF
Chọn đáp án B.
Câu 6
A. 180cm
B. 20cm
C. 30cm
D. 57cm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Hai tam giác ABC và MNP đồng dạng với nhau.
B. Chưa thể kết luận hai tam giác này đồng dạng.
C.
D. Tất cả sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. ΔAMC
B. ΔABC
C. ΔABP
D. ΔAPC
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. MN/BC = 3/7
B. Hai tam giác AMN và ABC đồng dạng với nhau
C. MN// BC
D. Tam giác AMC đồng dạng với tam giác ABN.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. 50cm
B. 60cm
C. 100cm
D. 80cm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. BC = 6cm
B. BC = 4cm
C. BC = 5cm
D. BC = 3cm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng k = 2
B.
C. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng
D. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. ΔAOB ⁓ ΔDOC với tỉ số đồng dạng
B.
C. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng
D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. 10cm; 15cm
B. 12cm; 16cm
C. 20cm; 10cm
D. 10cm; 20cm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. (I) đúng, (II) và (III) sai
B. (I) và (II) đúng, (III) sai
C. Cả (I), (II), (III) đều đúng
D. Cả (I), (II), (III) đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.