Cho tam giác vuông ABC ( = 90°). Lấy M bất kì trên cạnh Gọi E, F lần lượt là các điếm đối xứng với M qua AB và AC. Chứng minh: A là trung điểm của EF.
Câu hỏi trong đề: Bài tập: Đối xứng trục !!
Quảng cáo
Trả lời:
Sử dụng tính chất đối xứng trục => AE = AF (=AM) (1).
Sử dụng tính chất của tam giác cân . Từ đó chỉ ra được => E, A, F thằng hàng (2).
Từ (1) và (2) ta có điều phải chứng minh.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Sử dụng tính chất đối xứng trục kết hợp với chứng minh tam giác bằng nhau ta có được (Tính chất tam giác cân)
Þ ĐPCM.
b) Sử dụng tính chất đối xứng trục ta có PM = PE; QM = QF. Theo bất đẳng thức trong tam giacs MPQ, ta có:
PDMPQ = MP + PQ + QM= (PE + PQ) + QF ≥ EQ + QF ≥ EF.
Do M cố định, tam giác ABC cố định Þ E, F, I, K cố định. Vậy (PDMPQ)min = EF Û P º I, Q º K
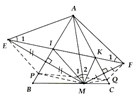
Lời giải
. Gọi A' là điểm đối xứng của A qua d Þ A' cố định.
Vì C Î d Þ CA = CA' (tính chất đối xứng trục). Ta có:
PDABC = AB + AC + BC
= AB + (CA' + CB) ≥ AB + BA' (không đổi. Dấu "=" xảy ra tức là chu vi tam giác nhỏ nhất khi C là giao điểm của d và BA'
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
