Câu hỏi:
02/04/2025 21,672Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D.
a) Chứng minh tứ giác BDCH là hình bình hành.
b) Tính số đo góc = 60°.
Câu hỏi trong đề: Bài tập: Hình bình hành !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
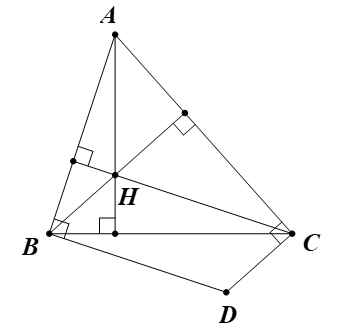
a) Ta có H là trực tâm của tam giác ABC.
Suy ra CH ⊥ AB.
Mà BD ⊥ AB (gt).
Do đó CH // BD.
Chứng minh tương tự, ta được BH // CD.
Vậy tứ giác BDCH là hình bình hành.
b) Ta có (cùng phụ với )
Lại có BH // CD (chứng minh trên)
Suy ra (cặp góc trong cùng phía)
Vậy .
Nhà sách vietjack
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC. Từ một điểm E trên cạnh AC vẽ đường thẳng song song với BC cắt AB tại F và đường thăng song song vói AB cắt BC tại D. Giả sử AE = BF, chứng minh:
a) Tam giác AED cân;
b) AD là phân giác của góc A.
Xem đáp án »
13/07/2024
34,530
Câu 2:
Cho hình bình hành ABCD. Gọi K, I lần lượt là trung điểm của các cạnh AB và CD. Gọi M và N lần lượt là giao điểm của AI và CK với BD. Chứng minh:
a) ∆ADM = CBN;
b) và IM//CN;
c) DM = MN = NB
Xem đáp án »
13/07/2024
14,418
Câu 3:
Cho tam giác ABC và O là một điểm thuộc miền trong của tam giác. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC, CA và L, M, N lần lượt là trung điểm của các đoạn OA, OB, OC. Chứng minh rằng các đoạn thẳng EL, FM và DN đồng quy
Xem đáp án »
13/07/2024
9,263
Câu 4:
Cho hình bình hành ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Qua điểm O, vẽ đường thẳng a cắt hai đường thẳng AD, BC lần lượt tại E, F. Qua O vẽ đưòng thẳng b cắt hai cạnh AB, CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành
Xem đáp án »
13/07/2024
5,688
Câu 5:
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA và I, K là trung điểm các đường chéo AC, BD. Chứng minh:
a) Các tứ giác MNPQ, INKQ là hình bình hành.
b) Các đường thẳng MP, NQ, IK đồng quy.
Xem đáp án »
13/07/2024
2,825
Câu 6:
Cho hình bình hành ABCD. Gọi E là trung điếm của AD, F là trung điểm của BC. Chứng minh:
a) BE = DF và
b) BE // DF
Xem đáp án »
13/07/2024
2,794
🔥 Đề thi HOT:
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 1)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
-
10 Bài tập Nhận biết hai hình đồng dạng, hai hình đồng dạng phối cảnh (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận