Câu hỏi:
13/07/2024 21,867Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC. Lấy E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.
a) Chứng minh tứ giác AHCE là hình chữ nhật.
b) Chứng minh HG = GK = KE.
Câu hỏi trong đề: Bài tập: Hình chữ nhật I. Tóm tắt lý thuyết !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Chứng minh: AHCE là hình bình hành; AH CE
Þ AHCE là hình chữ nhật.
b) Chứng minh G, K lần lượt là các trọng tâm của tam giác AHC, AEC và sử dụng tính chất 2 đường chéo của hình chữ nhật.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a) Tứ giác AMBQ là hình gì ?
b) Chứng minh rằng CH ^ AB.
c) Chứng minh tam giác PIQ cân.
Xem đáp án »
13/07/2024
32,673
Câu 2:
Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại h và K. Chứng minh rằng:
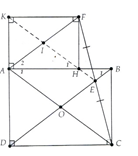
a) Tứ giác AHFK là hình chữ nhật;
b) AF song song với BD;
c) Ba điểm E, H, K thẳng hàng
Xem đáp án »
13/07/2024
28,870
Câu 3:
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M Î AB). Chứng minh tứ giác PCQM là hình chữ nhật.
Xem đáp án »
13/07/2024
21,896
Câu 4:
Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi M, N, P, Q lần lượt là trung điểm các đoạn thẳng AD, BD, AC, BC.
a) Chứng minh bốn điểm M, N, P, Q thẳng hàng.
b) Chứng minh tứ giác ABPN là hình thang cân.
c) Tìm một hệ thức liên hệ giữa AB và CD để ABPN là hình chữ nhật
Xem đáp án »
13/07/2024
7,426
Câu 5:
Cho hình chữ nhật ABCD. Điểm E thuộc cạnh AD, điểm F thuộc cạnh AB. Gọi I, K, M, N theo thứ tự là trung điểm của EF, FD, BE, BD. Chứng minh IN = KM
Xem đáp án »
13/07/2024
5,664
Câu 6:
Cho tam giác ABC. Gọi O là một điểm thuộc miền trong của tam giác. M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB.
a) Chứng minh tứ giác MNPQ là hình bình hành.
b) Xác định vị trí của điểm O để tứ giác MNPQ là hình chữ nhật
Xem đáp án »
13/07/2024
5,245
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luậnホアン・タイン・ダット
20:23 - 27/08/2024
Tuổi lồn
ホアン・タイン・ダット
20:29 - 27/08/2024
Địt cụ xóa comment của bố ah
ホアン・タイン・ダット
20:20 - 27/08/2024
Như đầu buồi giải thì giải cụ nó ra còn để phương pháp con mẹ mày