Cho đường thẳng (d): mx + 2y = 4
1. Vẽ đường thẳng khi m = 2
2. Tìm m để đường thẳng (d)
a) Cắt hai trục tọa độ tại hai điểm phân biệt
b) Song song với Ox
c) Song song với Oy
d) Song song với đường thẳng $Δ : x + y = 6$
e) Có hướng đi lên
f) Có hướng đi xuống
3. Chứng minh rằng khi m thay đổi, đường thẳng (d) luôn đi qua một điểm cố định

Xem lời giải

Câu hỏi trong đề: Bài tập ôn tập chương 3 đại số 9 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

1. Với m = 2, ta có $2 x + 2 y = 4 \Leftrightarrow y = - x + 2$

Với $x = 0 \Rightarrow y = 2$ , với $y = 0 \Rightarrow x = 4$

Đồ thị hàm số y = -x + 4 là một đường thẳng đi qua (0;4) và (4;0)

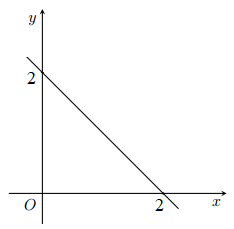
2. Xét phương trình $y = - \frac{m}{2} x + 2$ . Ta có

a) (d) cắt hai trục tọa độ tại 2 điểm phân biệt $\Leftrightarrow - \frac{m}{2} \neq 0 \Leftrightarrow m \neq 0$

b) (d) song song với Ox $\Leftrightarrow - \frac{m}{2} = 0 \Leftrightarrow m = 0$

c) (d) song song với Oy $\Leftrightarrow \{\begin{matrix} m \neq 0 \\ - \frac{2}{m} = 0 \end{matrix}$ (vô nghiệm)

Vậy không tồn tại m để (d) // Oy

d) (d) // $Δ \Leftrightarrow - \frac{m}{2} = - 1 \Leftrightarrow m = 2$

e) (d) có hướng đi lên $\Leftrightarrow - \frac{m}{2} > 0 \Leftrightarrow m < 0$

f) (d) có hướng đi xuống $\Leftrightarrow - \frac{m}{2} < 0 \Leftrightarrow m > 0$

3. Giả sử là điểm cố định mà đường thẳng luôn đi qua. Khi đó ta có:

${mx}_{0} + 2 y_{0} = 4 \forall m \Leftrightarrow \{\begin{matrix} x_{0} = 0 \\ 2 y_{0} - 4 = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x_{0} = 0 \\ y_{0} = 2 \end{matrix}$

Vậy M (0;2) là điểm cố định mà đường thẳng luôn đi qua khi m thay đổi.

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong các cặp số (-2;1); (0;2); (-1;0); (1,5;3); (4;-3) cặp số nào là nghiệm của phương trình?
a) 5x + 4y = 8
b) 3x + 5y = -3

Xem đáp án

Lời giải

a. Xét phương trình 5x + 4y = 8

- Với cặp số (-2;1). Ta có 5(-2) + 4.1 = -6 $\neq$ 8.

Do đó cặp số (-2;1) không là nghiệm của phương trình.

- Với cặp số (0;2). Ta có 0 + 4.2 = 8.

Do đó cặp số (0;2) là nghiệm của phương trình.

- Với cặp số (-1;0). Ta có (-1) + 4.0 = -5 $\neq$ 8.

Do đó cặp số (-1;0) không là nghiệm của phương trình.

- Với cặp số (1,5;3). Ta có 1,5 + 4.3 = 19,5 $\neq$ 8.

Do đó cặp số (1,5;3) không là nghiệm của phương trình.

- Với cặp số (4;-3). Ta có 4 + 4.(-3) = 8.

Do đó cặp số (4;-3) là nghiệm của phương trình.

b. Xét phương trình 3x + 5y = -3

- Các cặp (-1;0); (4;-3) là nghiệm của phương trình.

- Các cặp (-2;1); (0;2); (1,5;3) không là nghiệm của phương trình.

Câu 2

Tìm nghiệm nguyên của các phương trình:
a) x - 3y = 4
b) 3x + y = 6
c) 4x - 5y = 8

Xem đáp án

Lời giải

a) Biến đổi phương trình về dạng x = 3y + 4
Nhận xét rằng, với mọi y $\in Z$ , ta luôn có x = 3y + 4 $\in Z$
Vậy phương trình có vô số nghiệm nguyên thỏa mãn (3y +4;y) với y $\in Z$
b) Biến đổi phương trình về dạng y = -3x + 6
Nhận xét rằng, với mọi x $\in Z$ , ta luôn có y = -3x + 6 $\in Z$
Vậy phương trình có vô số nghiệm nguyên thỏa mãn (x;-3x + 6) với x $\in Z$
c) Biến đổi phương trình về dạng 4x = 5y + 8 <=> x = y + 2 + $\frac{y}{4}$ (1)

Đặt k = $\frac{y}{4}$ , k $\in Z$ <=> y = 4k, k $\in Z$
Thay y = 4k vào (1) ta được x = 4k + 2 + k = 5k + 2 $\in Z$ , k $\in Z$
Vậy phương trình có vô số nghiệm nguyên thỏa mãn (5k +2;4k) với kZ

Câu 3