Câu hỏi:
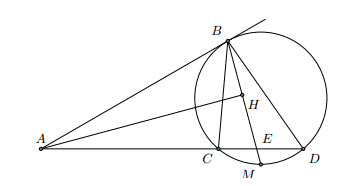
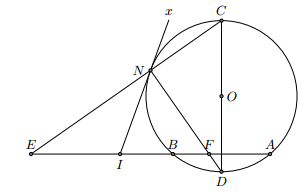
11/07/2024 3,185Cho nhọn và AB < AC nội tiếp đường tròn tâm O. Gọi D, E, F lần lượt là điểm chính giữa của các cung nhỏ AB, BC, CA. Tiếp tuyến tại A của đường tròn cắt các đường thẳng BC và DF lần lượt tại M và N. Gọi P và Q lần lượt là giao điểm của đường thẳng BC với đường thẳng DF và AE.
a) Chứng minh rằng
b) Chứng minh rằng MA = MQ, MN = MP
Câu hỏi trong đề:
Bài tập ôn tập chương 3 hình học 9 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
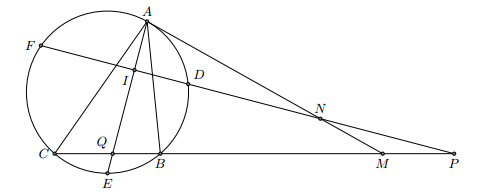
Trước hết, từ giả thiết “D, E, F lần lượt là điểm chính giữa của các cung nhỏ AB, BC, CA” ta được:
a) Gọi I là giao điểm của AE và DF, ta có ngay:
b) Xét sử dụng định lí về góc tạo bởi tia tiếp tuyến với một dây và góc có đỉnh ở bên trong đường tròn ta có
Xét , sử dụng định lí về góc có đỉnh ở bên ngoài đường tròn và hai góc đối đỉnh. Ta có:
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Từ một điểm A ở bên ngoài đường tròn (O) ta vẽ tiếp tuyến AB và cát tuyến ACD. Vẽ dây BM vuông góc với tia phân giác của góc BAC, dây này cắt CD tại E. Chứng minh rằng:
a) BM là tia phân giác của góc CBD
b) = ME.MB
Xem đáp án »
12/07/2024
17,460
Câu 2:
Cho đường tròn (O) và một dây AB. Vẽ đường kính CD vuông góc với AB (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy một điểm N. các đường thẳng CN và DN lần lượt cắt đường thẳng AB tại E và F. Tiếp tuyến của đường tròn tại N cắt đường thẳng AI tại I. Chứng minh rằng:
a) Các tam giác và là tam giác cân.
b) AI = (AE + AF)
Xem đáp án »
12/07/2024
10,577
Câu 3:
Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Lấy điểm M thuộc tia đối của tia BC. Gọi I là giao điểm của MA với đường tròn. Chứng minh rằng:
a)
b) AM.AI =
Xem đáp án »
12/07/2024
5,447
Câu 4:
Cho đường tròn (O), đường kính AB vuông góc với dây CD. Qua điểm M thuộc cung AD, kẻ tiếp tuyến với đường tròn, cắt CD ở I. Gọi E là giao điểm của BM và CD.
a) Chứng minh rằng IM = IE
b) Gọi F là giao điểm của AM và CD. Chứng minh rằng
Xem đáp án »
12/07/2024
4,145
Câu 5:
Cho đường tròn (O) đường kính AB, cung CD = nằm cùng phía đối với AB (D thuộc cung BC). Gọi E là giao điểm của AC và BD, F là giao điểm của AD và BC. Tính ,
Xem đáp án »
11/07/2024
3,418
Câu 6:
Từ một điểm M ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến MB, MC. Vẽ đường kính BOD. Hai đường thẳng CD và MB cắt nhau tại A. Chứng minh rằng M là trung điểm của AB.
Xem đáp án »
28/12/2020
2,861
về câu hỏi!