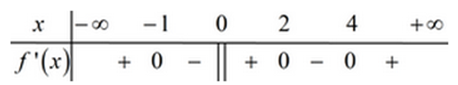Câu hỏi:

23/04/2022 1,454

Cho hàm số $y = a x^{4} + b x^{2} + c$ có đồ thị như hình vẽ bên.

Mệnh đề nào dưới đây đúng?

A. $a < 0, b < 0, c < 0$

B. $a < 0, b > 0, c < 0$

C. $a > 0, b < 0, c < 0$

D. $a > 0, b < 0, c > 0$

Xem lời giải

Câu hỏi trong đề: [Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương pháp giải:

Dựa vào đồ thị hàm số để nhận xét các điểm mà đồ thị hàm số đã đi qua, các điểm cực trị của hàm số để suy ra dấu của $a, b, c .$

Cho hàm số $y = a x^{4} + b x^{2} + c (a \neq 0)$ ta có:

+) Hàm số có một cực trị $\Leftrightarrow a b \geq 0$

+) Hàm số có ba cực trị $\Leftrightarrow a b < 0$

Giải chi tiết:

Dựa vào đồ thị hàm số ta thấy nét cuối của đồ thị đi xuống dưới

$\Rightarrow a < 0$ ⇒ loại đáp án C và D.

Đồ thị hàm số có 3 điểm cực trị $\Rightarrow a b < 0 \Rightarrow b > 0.$

Đáp án B

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong bài thi thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua một sông để tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi của chiến sĩ bằng một phần ba vận tốc chạy trên bộ. Hãy cho biết chiến sĩ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất? Biết dòng sông là thẳng, mục tiêu cách chiến sĩ 1km theo đường chim bay và chiến sĩ cách bờ bên kia 100m.

A. $\frac{200 \sqrt{2}}{3} (m)$

B. $60 \sqrt{5} (m)$

C. $\frac{200 \sqrt{3}}{3} (m)$

D. $75 \sqrt{2} (m)$

Lời giải

Phương pháp giải:

Ta có hình vẽ, khi đó chiến sĩ ở vị trí A, mục tiêu ở vị trí C.

Quãng đường chiến sĩ phải bơi là AD, quãng đường chiến sĩ phải chạy bộ là DC.

Ta có: $B C = \sqrt{A C^{2} - A B^{2}} = \sqrt{1000^{2} - 100^{2}} = 300 \sqrt{11} (m) .$

Đặt $B D = x (m), (0 < x < 300 \sqrt{11}) .$

⇒ Quãng đường chiến sĩ phải bơi là: $A D = \sqrt{A B^{2} + B D^{2}} = \sqrt{x^{2} + 100^{2}} (m) .$

Quãng đường chiến sĩ phải chạy bộ là: $C D = B C - B D = 300 \sqrt{11} - x (m) .$

⇒ Thời gian chiến sĩ đến được mục tiêu là: $A D = \sqrt{A B^{2} + B D^{2}} = \sqrt{x^{2} + 100^{2}} (m) .$

Tìm x để $t (x)$ đạt $M i n$ rồi suy ra quãng đường chiễn sĩ phải bơi.

Giải chi tiết:

Trong bài thi thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi (ảnh 1)

Gọi vận tốc của chiến sĩ khi bơi là $a (m / s), (a > 0) .$

⇒ Vận tốc của chiến sĩ khi chạy bộ là: $3 a (m / s) .$

Ta có hình vẽ, khi đó chiến sĩ ở vị trí A, mục tiêu ở vị trí C.

Quãng đường chiến sĩ phải bơi là AD, quãng đường chiến sĩ phải chạy bộ là DC.

Ta có: $B C = \sqrt{A C^{2} - A B^{2}} = \sqrt{1000^{2} - 100^{2}} = 300 \sqrt{11} (m) .$

Đặt $B D = x (m), (0 < x < 300 \sqrt{11}) .$

⇒ Quãng đường chiến sĩ phải bơi là: $A D = \sqrt{A B^{2} + B D^{2}} = \sqrt{x^{2} + 100^{2}} (m) .$

Quãng đường chiến sĩ phải chạy bộ là: $C D = B C - B D = 300 \sqrt{11} - x (m) .$

⇒ Thời gian chiến sĩ đến được mục tiêu là: $t = \frac{A D}{a} + \frac{D C}{3 a} = \frac{\sqrt{x^{2} + 100^{2}}}{a} + \frac{300 \sqrt{11} - x}{3 a}$

$= \frac{1}{3 a} (3 \sqrt{x^{2} + 100^{2}} + 300 \sqrt{11} - x)$

Xét hàm số: $f (x) = 3 \sqrt{x^{2} + 100^{2}} - x + 300 \sqrt{11}$ trên $(0; 300 \sqrt{11})$ ta có:

$f^{'} (x) = \frac{3 x}{2 \sqrt{x^{2} + 100^{2}}} - 1 \Rightarrow f^{'} (x) = 0$

$\Leftrightarrow 3 x = 2 \sqrt{x^{2} + 100^{2}} \Leftrightarrow 9 x^{2} = 4 x^{2} + {4.100}^{2}$

$\Leftrightarrow 5 x^{2} = {4.100}^{2}$

$\Leftrightarrow x^{2} = \frac{4}{5} {.100}^{2} \Leftrightarrow x = \frac{2 \sqrt{5}}{5} .100 = 40 \sqrt{5} (t m)$

⇒ Quãng đường bơi mà chiến sĩ phải bơi để đến được mục tiêu nhanh nhất là:

$A D = \sqrt{x^{2} + 100^{2}} = \sqrt{\frac{4}{5} {.100}^{2} + 100^{2}}$ $= \sqrt{\frac{9}{5} {.100}^{2}} = 60 \sqrt{5} m .$

Đáp án B

Câu 2

Cho hàm số $y = f (x)$ liên tục trên $ℝ$ và có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho có bao nhiêu điểm cực trị?

A.4

B.2

C.3

D.1

Lời giải

Phương pháp giải:

Xác định các điểm mà tại đó hàm số liên tục và qua đó đạo hàm đổi dấu.

Giải chi tiết:

Dựa vào BXD đạo hàm ta thấy:

Hàm số liên tục tại các điểm $x = - 1, x = 0, x = 2, x = 4$ (do hàm số liên tục trên $ℝ$ ) và qua các điểm đó đạo hàm đều đổi dấu.

Vậy hàm số $y = f (x)$ có 4 điểm cực trị.

Đáp án A

Câu 3

Tìm giá trị thực của tham số m để đường thẳng $d : y = (3 m + 1) x + 3 + m$ vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y = x^{3} - 3 x^{2} - 1$ .

A. $m = \frac{1}{6}$

B. $m = - \frac{1}{6}$

C. $m = \frac{1}{3}$

D. $m = - \frac{1}{3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Hàm số $y = | {(x - 1)}^{3} (x + 1) |$ có bao nhiêu điểm cực trị?

A.3

B.1

C.2

D.4

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số $y = x^{3} - \frac{3}{2} x^{2} + 1.$ Gọi M là giá trị lớn nhất của hàm số trên $(- 25; \frac{11}{10}) .$ Tìm M.

A. $M = 1$

B. $M = \frac{1}{2}$

C. $M = 0$

D. $M = \frac{129}{250}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Khoảng cách giữa hai điểm cực của đồ thị hàm số $y = - x^{3} + 3 x + 2$ bằng:

A. $2 \sqrt{5}$

B. $2 \sqrt{3}$

C. $3 \sqrt{5}$

D.2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Một hộp đựng 40 tấm thẻ được đánh số thứ tự từ 1 đến 40. Rút ngẫu nhiên 10 tấm thẻ. Tính xác suất để lấy được 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó có đúng một thẻ mang số chia hết cho 6.

A. $\frac{126}{1147}$

B. $\frac{252}{1147}$

C. $\frac{26}{1147}$

D. $\frac{12}{1147}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho hàm số y=ax4+bx2+c có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

Cho hàm số y=f(x) liên tục trên ℝ và có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho có bao nhiêu điểm cực trị?

Tìm giá trị thực của tham số m để đường thẳng d:y=(3m+1)x+3+m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y=x3−3x2−1.

Hàm số y=|(x−1)3(x+1)| có bao nhiêu điểm cực trị?

Cho hàm số y=x3−32x2+1. Gọi M là giá trị lớn nhất của hàm số trên (−25;1110). Tìm M.

Khoảng cách giữa hai điểm cực của đồ thị hàm số y=−x3+3x+2 bằng:

Một hộp đựng 40 tấm thẻ được đánh số thứ tự từ 1 đến 40. Rút ngẫu nhiên 10 tấm thẻ. Tính xác suất để lấy được 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó có đúng một thẻ mang số chia hết cho 6.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hàm số $y = a x^{4} + b x^{2} + c$ có đồ thị như hình vẽ bên.

Mệnh đề nào dưới đây đúng?

Cho hàm số $y = f (x)$ liên tục trên $ℝ$ và có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho có bao nhiêu điểm cực trị?

Tìm giá trị thực của tham số m để đường thẳng $d : y = (3 m + 1) x + 3 + m$ vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y = x^{3} - 3 x^{2} - 1$ .

Hàm số $y = | {(x - 1)}^{3} (x + 1) |$ có bao nhiêu điểm cực trị?

Cho hàm số $y = x^{3} - \frac{3}{2} x^{2} + 1.$ Gọi M là giá trị lớn nhất của hàm số trên $(- 25; \frac{11}{10}) .$ Tìm M.

Khoảng cách giữa hai điểm cực của đồ thị hàm số $y = - x^{3} + 3 x + 2$ bằng: