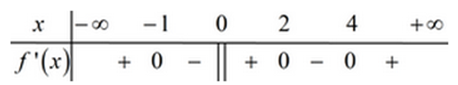Cho hình chóp đều có độ dài cạnh đáy bằng a , cạnh bên bằng . Gọi là tâm của đáy , là khoảng cách từ A đến mặt phẳng và là khoảng cách từ O đến mặt phẳng . Tính .
A.
B.
C.
D.
Quảng cáo
Trả lời:
Phương pháp giải:
- Gọi M là trung điểm của BC, xác định .
- Sử dụng định lí Pytago và công thức diện tích tam giác, tính .
- Sử dụng công thức: , so sánh và .
Giải chi tiết:
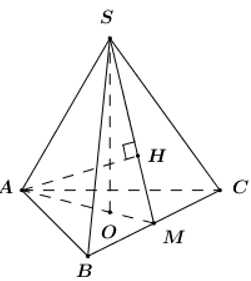
Gọi M là trung điểm của BC ta có: .
Trong kẻ ta có: .
Vì đều cạnh nên .
Áp dụng định lí Pytago trong tam giác vuông có: .
Áp dụng định lí Pytago trong tam giác vuông có: .
Ta có: .
.
Ta có:
.
.
Vậy .
Đáp án A
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp giải:
Ta có hình vẽ, khi đó chiến sĩ ở vị trí A, mục tiêu ở vị trí C.
Quãng đường chiến sĩ phải bơi là AD, quãng đường chiến sĩ phải chạy bộ là DC.
Ta có:
Đặt
⇒ Quãng đường chiến sĩ phải bơi là:
Quãng đường chiến sĩ phải chạy bộ là:
⇒ Thời gian chiến sĩ đến được mục tiêu là:
Tìm x để đạt rồi suy ra quãng đường chiễn sĩ phải bơi.
Giải chi tiết:
Gọi vận tốc của chiến sĩ khi bơi là
⇒ Vận tốc của chiến sĩ khi chạy bộ là:
Ta có hình vẽ, khi đó chiến sĩ ở vị trí A, mục tiêu ở vị trí C.
Quãng đường chiến sĩ phải bơi là AD, quãng đường chiến sĩ phải chạy bộ là DC.
Ta có:
Đặt
⇒ Quãng đường chiến sĩ phải bơi là:
Quãng đường chiến sĩ phải chạy bộ là:
⇒ Thời gian chiến sĩ đến được mục tiêu là:
Xét hàm số: trên ta có:
⇒ Quãng đường bơi mà chiến sĩ phải bơi để đến được mục tiêu nhanh nhất là:
Lời giải
Phương pháp giải:
Xác định các điểm mà tại đó hàm số liên tục và qua đó đạo hàm đổi dấu.
Giải chi tiết:
Dựa vào BXD đạo hàm ta thấy:
Hàm số liên tục tại các điểm (do hàm số liên tục trên ) và qua các điểm đó đạo hàm đều đổi dấu.
Vậy hàm số có 4 điểm cực trị.
Đáp án A
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.