Câu hỏi:
25/04/2022 820Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp 12A, 3 học sinh lớp 12B và 5 học sinh lớp 12C thành một hàng ngang. Xác suất để trong 10 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau bằng
Quảng cáo
Trả lời:
Giải bởi Vietjack
Số cách xếp 10 học sinh vào 10 vị trí: \(n\left( \Omega \right) = 10!\) cách.
Gọi \(A\) là biến cố: “Trong 10 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau”.
Sắp xếp 5 học sinh lớp 12C vào 5 vị trí, có 5! cách.
Ứng mỗi cách xếp 5 học sinh lớp 12C sẽ có 6 khoảng trống gồm 4 vị trí ở giữa và hai vị trí hai đầu để xếp các học sinh còn lại
|
C1 |
C2 |
C3 |
C4 |
C5 |
TH1: Xếp 3 học sinh lớp 12B vào 4 vị trí trống ở giữa (không xếp vào hai đầu), có \[A_4^3\] cách.
Ứng với mỗi cách xếp đó, chọn lấy 1 trong 2 học sinh lớp 12A xếp vào vị trí trống thứ 4 (để hai học sinh lớp 12C không được ngồi cạnh nhau), có 2 cách.
Học sinh lớp 12A còn lại có 8 vị trí để xếp, có 8 cách.
Theo quy tắc nhân, ta có \(5!.A_4^3.2.8\) cách.
TH2: Xếp 2 trong 3 học sinh lớp 12B vào 4 vị trí trống ở giữa và học sinh còn lại xếp vào hai đầu, có \(C_3^1.2.A_4^2\) cách.
Ứng với mỗi cách xếp đó sẽ còn 2 vị trí trống ở giữa, xếp 2 học sinh lớp 12A vào vị trí đó, có 2 cách.
Theo quy tắc nhân, ta có \(5!.C_3^1.2.A_4^2.2\) cách.
Do đó số cách xếp không có học sinh cùng lớp ngồi cạnh nhau là:
\(n\left( A \right) = 5!.2.8 + 5!.C_3^1.2.A_4^2.2 = 63360\) cách.
Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{63360}}{{10!}} = \frac{{11}}{{630}}.\)
Đáp án B.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
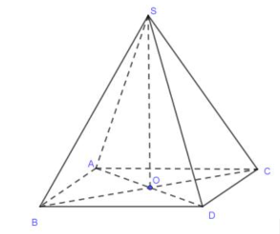
Vì \(AB//CD\) nên \(\left( {\widehat {SA;CD}} \right) = \left( {\widehat {SA;AB}} \right)\) mà \(S.ABCD\) là chóp tứ giác đều và \(SA = AB = a\) nên \(\Delta SAB\) đều. Vậy \(\widehat {\left( {SA;AB} \right)} = {60^0},\) khi đó góc giữa \(SA\) và \(CD\) là \({60^0}\) nên chọn đáp án A.
Lời giải
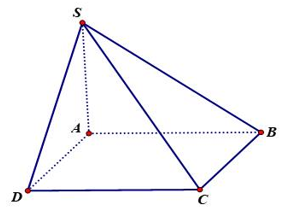
Vì \(AB//CD\) nên \(\left( {\widehat {SC;AB}} \right) = \left( {\widehat {SC;CD}} \right) = \widehat {SCD}.\)
Ta có \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot SD\)
\( \Rightarrow \Delta SCD\) vuông tại D.
Trong tam giác vuông \(SAD\) có
\(SD = \sqrt {S{A^2} + A{D^2}} = \sqrt {2{a^2} + 4{a^2}} = a\sqrt 6 .\)
Trong tam giác vuông \(SCD\) có
\(\tan \widehat {SCD} = \frac{{SD}}{{CD}} = \frac{{a\sqrt 6 }}{{a\sqrt 2 }} = \sqrt 3 \Rightarrow \widehat {SCD} = {60^0}.\)
Vậy góc giữa hai đường thẳng \(SC\) và \(AB\) bằng \({60^0}.\)
Đáp án B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
45 bài tập Xác suất có lời giải
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 11)