Câu hỏi:
27/04/2022 720Cho một đa giác đều có 18 đỉnh nội tiếp đường tròn tâm \(O.\) Gọi \(X\) là tập hợp tất cả các tam giác có 3 đỉnh trùng với 3 trong số 18 đỉnh của đa giác đã cho. Chọn 1 tam giác trong tập hợp \(X.\) Xác suất để tam giác được chọn là tam giác cân bằng
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn ngẫu nhiên 3 trong số 18 đỉnh của đa giác ta được 1 tam giác nên \(n\left( \Omega \right) = C_{18}^3 = 816.\)
Vì đa giác đã cho là đa giác đều có 18 đỉnh nên từ mỗi đỉnh có thể tìm ra 8 cặp điểm để cùng với nó tạo ra 1 tam giác cân, trong đó có 1 tam giác đều. Từ 18 đỉnh của đa giác đều có thể tạo ra 6 tam giác đều. Vậy số tam giác cân và đều mà 18 đỉnh của đa giác đều đó tạo ra là: \(18.7 + 6 = 132\)
Xác suất cần tìm là:
Đáp án D
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
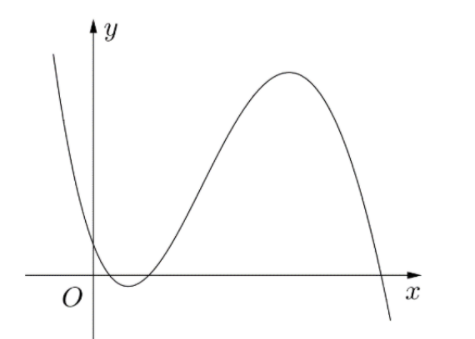
Từ đồ thị ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0.\)
Gọi \({x_1}\) và \({x_2}\) lần lượt là hai điểm cực trị của hàm số đã cho \(\left( {{x_1} < {x_2}} \right).\)
Từ đồ thị ta thấy: \({x_1} + {x_2} >0 \Rightarrow ab < 0 \Rightarrow b >0.\)</>
Và: \({x_1}.{x_2} >0 \Rightarrow ac >0 \Rightarrow c >0.\)
Đồ thị hàm số giao với trục tung tại điểm có tung độ \(y \Rightarrow d >0.\)
Vậy trong các số \(a,b,c,d\) có hai số dương.
Đáp án D
Lời giải
Tập xác định \(D = \mathbb{R}\)
\(y' = 3{x^2} - 6\left( {2m + 1} \right)x + 12m + 5\)
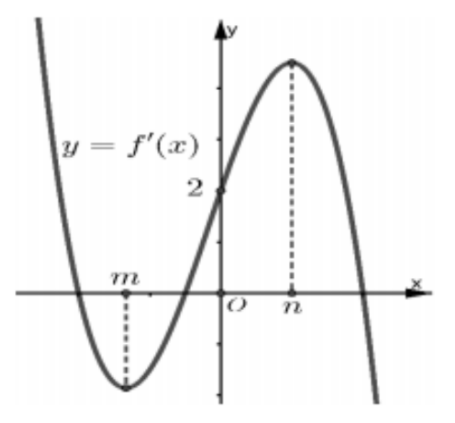
Hàm số đồng biến trong khoảng \(\left( {2; + \infty } \right)\) khi \(y' \ge 0,\forall x \in \left( {2; + \infty } \right).\)
\( \Leftrightarrow 3{x^2} - 6\left( {2m + 1} \right)x + 12m + 5 \ge 0\forall x \in \left( {2; + \infty } \right).\)
\(3{x^2} - 6\left( {2m + 1} \right)x + 12m + 5 \ge 0 \Leftrightarrow m \le \frac{{3{x^2} - 6x + 5}}{{12\left( {x - 1} \right)}},\forall x \in \left( {2; + \infty } \right)\)
Xét hàm số \(g\left( x \right) = \frac{{3{x^2} - 6x + 5}}{{12\left( {x - 1} \right)}},\forall x \in \left( {2; + \infty } \right).\)
\(g'\left( x \right) = \frac{{3{x^2} - 6x + 1}}{{12{{\left( {x - 1} \right)}^2}}} >0,\forall x \in \left( {2; + \infty } \right) \Rightarrow \) Hàm số \(g\left( x \right)\) đồng biến trong khoảng \(\left( {2; + \infty } \right).\)
Do đó: \(m \le g\left( x \right),\forall x \in \left( {2; + \infty } \right) \Rightarrow m \le g\left( 2 \right) \Leftrightarrow m \le \frac{5}{{12}}.\)
Vì \(0 < m \le \frac{5}{{12}}.\) Do đó không có giá trị nguyên dương nào của \(m\) thỏa mãn bài toán.
Đáp án C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận