Nhà bạn Minh cần khoan một cái giếng nước. Biết rằng giá tiền của mét khoan đầu tiên là 200.000đ và kể từ mét khoan thứ hai, giá tiền của mỗi mét sau tăng thêm 7% so với giá tiền của mét khoan ngay trước nó. Hỏi nếu nhà bạn An khoan cái giếng sâu 30m thì hết bao nhiêu tiền (làm tròn đến hàng nghìn)?
A. \(18895000\)đ.
B. \(1422851\)đ.
C. \(18892000\)đ.
D. \(18892200\)đ.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Bài toán tổng quát:
Giả sử giá tiền của mét khoan đầu tiên là \(x\) (đồng) và giá tiền của mỗi mét sau tăng thêm \(y\% \) so với giá tiền của mét khoan ngay trước đó \(\left( {x >0;y >0} \right).\) Ta có:
* Giá tiền mét khoan đầu tiên là \({S_1} = x\) (đồng)
* Giá tiền mét khoan thứ hai là \({S_2} = x + \frac{y}{{100}}.x = \frac{{y + 100}}{{100}}.x\) (đồng)
* Giá tiền mét khoan thứ ba là \({S_3} = {S_2} + \frac{y}{{100}}.{S_2} = \frac{{y + 100}}{{100}}.{S_2} = {\left( {\frac{{y + 100}}{{100}}} \right)^2}.x\) (đồng)
* Giá tiền của mét khoan thứ ba là \({S_4} = {S_3} + \frac{y}{{100}}.{S_3} = \frac{{y + 100}}{{100}}.{S_3} = {\left( {\frac{{y + 100}}{{100}}} \right)^3}.x\) (đồng)
…………………………………………………………………………………………
* Giá tiền của mét khoan thứ \(n\) là \({S_n} = {S_{n - 1}} + \frac{y}{{100}}.{S_{n - 1}} = \frac{{y + 100}}{{100}}.{S_{n - 1}} = {\left( {\frac{{y + 100}}{{100}}} \right)^{n - 1}}.x\) (đồng)
\( \Rightarrow \) Giá tiền để khoan cái giếng sâu \(n\) mét là:
\(S = {S_1} + {S_2} + {S_3} + ... + {S_n} = \left[ {1 + \frac{{y + 100}}{{100}} + {{\left( {\frac{{y + 100}}{{100}}} \right)}^2} + ... + {{\left( {\frac{{y + 100}}{{100}}} \right)}^{n - 1}}} \right].x\)
Đặt \(k = \frac{{y + 100}}{{100}} \Rightarrow S = \left( {1 + k + {k^2} + ... + {k^{n - 1}}} \right).x = \frac{{x\left( {1 - {k^n}} \right)}}{{1 - k}}\)
\(k = 1,07\) và \({S_{30}} = \frac{{200000.\left( {1 - {{1.07}^{30}}} \right)}}{{1 - 1,07}} \approx 18892000\) (đồng)
Vậy nếu nhà bạn An khoan cái giếng sâu 30 m thì hết 18892000 đồng.
Đáp án C
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[\frac{9}{{95}}\].
B. \[\frac{{127}}{{380}}\].
C. \[\frac{{11}}{{380}}\].
D. \[\frac{{11}}{{190}}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi không gian mẫu là \(\Omega .\)
Chọn 3 từ 40 thẻ có \(C_{40}^3\) cách.
\( \Rightarrow n\left( \Omega \right) = C_{40}^3 = 9880.\)
Gọi A: “Tổng 3 số ghi trên thẻ là một số chia hết cho 3”.
Các số chia hết cho 3 từ 1 đến 40 là: \(\left\{ {3;6;9;...30;33;36;39} \right\}:\) có 13 số.
Các số chia cho 3 dư 1 từ 1 đến 40 là: \(\left\{ {1;4;7;...31;34;37;40} \right\}:\) có 14 số.
Các số chia cho 3 dư 2 từ 1 đến 40 là: \(\left\{ {2;5;8;...32;35;38} \right\}:\) có 13 số.
Trường hợp 1:3 số cùng chia hết cho 3; chia cho 3 dư 1; chia cho 3 dư 2:
Có: \(C_{13}^3 + C_{13}^3 + C_{14}^3 = 286 + 286 + 364 = 936\) cách.
Trường hợp 2:1 số chia hết cho 3, 1 số chia cho 3 dư 1 và 1 số chia cho 3 dư 2:
Có: \(C_{13}^1.C_{13}^1.C_{14}^1 = 2366\) cách.
Vậy số cách chọn để được tổng 3 số chia hết cho 3 là: \(936 + 2366 = 3302\) cách.
\( \Rightarrow n\left( A \right) = 3302.\)
Xác suất biến cố A là: \(p\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{3302}}{{9880}} = \frac{{127}}{{380}}.\)
Đáp án B
Câu 2
A. \[y = 2{x^4} - {x^2} + 1\].
B. \[y = - {x^4} + {x^2} + 1\].
C. \[y = - {x^4} + 2{x^2} + 1\].
D. \[y = {x^4} - 2{x^2} + 1\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
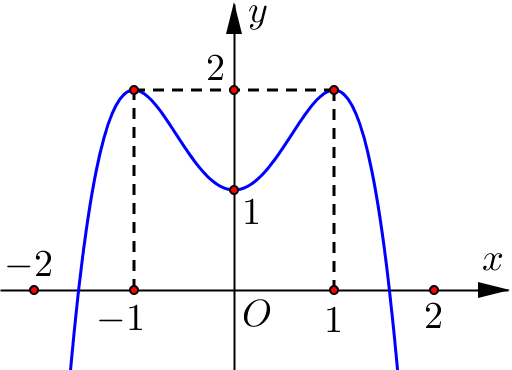
Dựa vào đồ thị ta có đồ thị trên là đồ thị hàm bậc bốn trùng phương có bề lõm hướng xuống nên hệ số \(a < 0\) nên loại đáp án A và D.
Xét điểm \(\left( {1;2} \right)\) thuộc đồ thị hàm số trên.
Thay \(\left( {1;2} \right)\) vào \(y = - {x^4} + {x^2} + 1\) ta được 2 =1 (vô lý).
Thay \(\left( {1;2} \right)\) vào \(y = - {x^4} + 2{x^2} + 1\) ta được 2 = 2 (đúng).
Nên đồ thị trong hình vẽ trên là đồ thị của hàm số \(y = - {x^4} + 2{x^2} + 1.\)
Đáp án A
Câu 3
A. \[V = \frac{{\sqrt {15} {a^3}}}{3}\].
B. \[V = \frac{{\sqrt 3 {a^3}}}{3}\].
C. \[V = 2\sqrt 3 {a^3}\].
D. \[V = \frac{{2\sqrt {15} {a^3}}}{3}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(3030\)
B. 2020
C. 3031
D. 4040
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[\frac{{2{a^3}\sqrt 3 }}{3}.\]
B. \[{a^3}\sqrt 3 .\]
C. \[\frac{{{a^3}\sqrt 3 }}{2}\]
D. \[\frac{{{a^3}\sqrt 3 }}{3}\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.
B. \({a^3}\).
C. \(\frac{2}{3}{a^3}\).
D. \(4{a^3}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[\frac{1}{5}\].
B. \[\frac{4}{5}\].
C. \[20\].
D. \[\frac{5}{4}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập