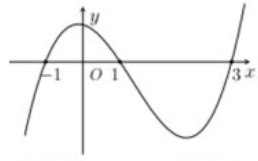
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) để đường thẳng \(y = m\) cắt đồ thị hàm số \(y = {x^3} - 3{x^2}\) tại 3 điểm phân biệt \(A,B,C\) \((B\) nằm giữa \(A\) và \(C)\) sao cho \(AB = 2BC.\) Tính tổng các phần tử thuộc \(S.\)
A. \( - 4.\)
B.\(\frac{{7 - \sqrt 7 }}{7}.\)
C. \( - 2.\)
Quảng cáo
Trả lời:
Phương trình hoành độ giao điểm của đường thẳng \(y = m\) và đồ thị hàm số \(y = {x^3} - 3{x^2}\) là \({x^3} - 3{x^2} - m = 0\left( * \right).\)
Gọi \({x_1},{x_2},{x_3}\left( {{x_1} < {x_2} < {x_3}} \right)\) lần lượt là 3 nghiệm của (*), theo giả thiết ta giả sử \(A\left( {{x_1};{y_1}} \right),B\left( {{x_2};{y_2}} \right),C\left( {{x_3};{y_3}} \right)\) khi đó
\(AB = 2BC \Leftrightarrow \left| {{x_2} - {x_1}} \right| = 2\left| {{x_3} - {x_2}} \right|\)
\( \Leftrightarrow {x_2} - {x_1} = 2\left( {{x_3} - {x_2}} \right)\)
\( \Leftrightarrow {x_1} + {x_2} + {x_3} = 4{x_2} - {x_3} \Leftrightarrow {x_3} = 4{x_2} - 3\) (theo ĐL Vi-et cho PT(*) có \({x_1} + {x_2} + {x_3} = 3).\)
Thay nghiệm \({x_3} = 4{x_2} - 3\) vào (*) ta có phương trình \({\left( {4{x_2} - 3} \right)^3} - 3{\left( {4{x_2} - 3} \right)^2} = m\)
Lại có \({x_2}\) cũng là nghiệm của \(\left( * \right)\) nên \(x_2^3 - 3x_2^2 = m\) do đó ta có phương trình
\({\left( {4{x_2} - 3} \right)^3} - 3{\left( {4{x_2} - 3} \right)^2} = x_2^3 - 3x_2^2\)
\( \Leftrightarrow 64x_2^3 - 144x_2^2 + 108x_2^{} - 27 - 3\left( {16x_2^2 - 24{x_2} + 9} \right) = x_2^3 - 3x_2^2\)
\( \Leftrightarrow 63x_2^3 - 189x_2^3 + 180{x_2} - 54 = 0\)
\( \Leftrightarrow 7x_2^3 - 21x_2^3 + 20{x_2} - 6 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}{x_2} = \frac{{7 + \sqrt 7 }}{7}\\{x_2} = 1\\{x_2} = \frac{{7 - \sqrt 7 }}{7}\end{array} \right.\)
Với \({x_2} = 1\) suy ra \({x_3} = 1\) (loại).
Với \({x_2} = \frac{{7 \pm \sqrt 7 }}{7} \Rightarrow m = - \frac{{48 \pm 20\sqrt 7 }}{{49}}.\)
Thử lại trực tiếp ta thấy \(m = - \frac{{98 + 20\sqrt 7 }}{{49}}\) và \(m = - \frac{{98 - 20\sqrt 7 }}{{49}}\) là thỏa mãn được yêu cầu bài toán.
Vậy \(S = \left\{ { - \frac{{98 - 20\sqrt 7 }}{{49}}; - \frac{{98 + 20\sqrt 7 }}{{49}}} \right\}\) và tổng các phần tử thuộc tập \(S\) là \( - 4.\)
Đáp án A
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
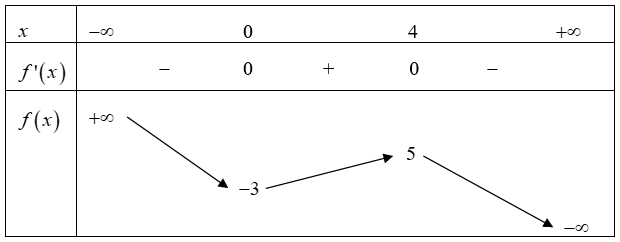
Đặt \(g\left( x \right) = 3{x^4} - 8{x^3} - 6{x^2} + 24x - m.\) Ta có số điểm cực trị của hàm số
\(y = \left| {3{x^4} - 8{x^3} + 24x - m} \right|\) bằng \(a + b.\) Với 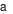 là số điểm cực trị của hàm \(g\left( x \right)\) và \(b\) là số nghiệm đơn (bội lẻ) của phương trình \(g\left( x \right) = 0.\)
là số điểm cực trị của hàm \(g\left( x \right)\) và \(b\) là số nghiệm đơn (bội lẻ) của phương trình \(g\left( x \right) = 0.\)
Xét hàm số ta có
\(g'\left( x \right) = 12{x^3} - 24{x^2} - 12x + 24 = 12\left( {x + 1} \right)\left( {x - 2} \right)\left( {x - 1} \right)\) suy ra hàm số \(g\left( x \right)\) có 3 điểm cực trị.
Xét phương trình
\(g\left( x \right) = 0 \Leftrightarrow g\left( x \right) = 3{x^4} - 8{x^3} - 6{x^2} + 24x - m = 0 \Leftrightarrow 3{x^4} - 8{x^3} - 6{x^2} + 24x = m.\) Đồ thị hàm số \(y = \left| {g\left( x \right)} \right|\) có 7 điểm cực trị khi phương trình \(g\left( x \right) = 0\) có đúng 4 nghiệm phân biệt tương đương với hai đồ thị hàm số \(y = 3{x^4} - 8{x^3} - 6{x^2} + 24x\) và \(y = m\) có 4 giao điểm phân biệt.
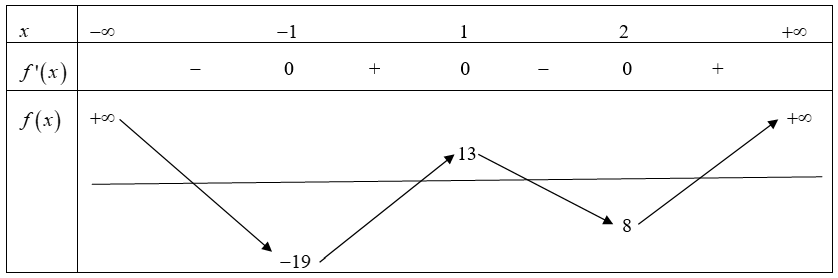
Mà \(m \in \mathbb{Z}\) nên \(m \in \left\{ {9,10,11,12} \right\}.\) Vậy tổng các giá trị của tham số \(m\) là
\(S = 9 + 10 + 11 + 12 = 42.\)
Đáp án A
Lời giải
Gọi \({A_0}\) là số tiền ban đầu bạn An mang đi gửi tiếp kiệm, \(r\) là lãi suất đem gửi, \(x\) là số tháng bạn An cần gửi tiết kiệm để thu được cả vốn lẫn lãi bằng hoặc vượt quá 1300000 đồng.
Vì bạn An gửi tiết kiệm không thời hạn nên số tiền gốc và lãi thu được của tháng này sẽ là tiền gốc hay chính là số tiền đem gửi tiết kiệm của tháng sau.
Vậy sau 1 tháng bạn An thu được cả gốc và lãi là \({A_0} + {A_0}.r = {A_0}{\left( {1 + r} \right)^3}.\)
Sau 2 tháng bạn An thu được số tiền cả gốc và lãi là \({A_0}\left( {1 + r} \right) + {A_0}\left( {1 + r} \right).r = {A_0}{\left( {1 + r} \right)^2}.\)
Sau \(x\) tháng bạn An thu được số tiền cả gốc và lãi là \({A_0}{\left( {1 + r} \right)^x}.\)
Vậy ta có
\(1300000 \le 1000000{\left( {1 + 0,0058} \right)^x} \Leftrightarrow x \ge {\log _{1,0058}}1,3 \approx 45,366.\)
Vậy bạn An phải gửi ít nhất là 46 tháng thì thu được cả vốn và lãi bằng hoặc vượt quá 1300000 đồng.
Đáp án A
Câu 3
A. \( - 4.\)
B.\( - 12{x^7}.\)
C.\(9{x^7}.\)
D. \( - 4{x^7}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\({45^0}.\)\(\angle SCA\)
B.\({30^0}.\)
C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.