Câu hỏi:
13/07/2024 5,933
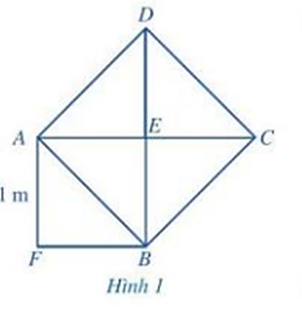
Quan sát Hình 1, ở đó hình vuông AEBF có cạnh bằng 1 m, hình vuông ABCD có cạnh AB là một đường chéo của hình vuông AEBF.
a) Tình diện tích của hình vuông ABCD.
b) Tính độ dài đường chéo AB.
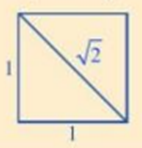
Lưu ý: là độ dài đường chéo của hình vuông có cạnh bằng 1.
Quan sát Hình 1, ở đó hình vuông AEBF có cạnh bằng 1 m, hình vuông ABCD có cạnh AB là một đường chéo của hình vuông AEBF.
a) Tình diện tích của hình vuông ABCD.
b) Tính độ dài đường chéo AB.
Lưu ý: là độ dài đường chéo của hình vuông có cạnh bằng 1.
Câu hỏi trong đề:
Bài tập Số vô tỉ. Căn bậc hai số học có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Quan sát Hình 1 ta thấy hình vuông ABCD được tạo thành từ 4 tam giác nhỏ bằng nhau nên diện tích hình vuông ABCD gấp 4 lần diện tích tam giác AEB.
Hình vuông AEBF là hình vuông có cạnh bằng 1 và tạo bởi hai tam giác là AEB và AFB nên diện tích của hình vuông AEBF gấp 2 lần diện tích của tam giác AEB.
Diện tích hình vuông AEBF có cạnh bằng 1 m là: 1.1 = 1 (m2).
Diện tích hình vuông AEBF gấp 2 lần diện tích tam giác AEB nên diện tích tam giác AEB là: 1 : 2 = (m2).
Diện tích hình vuông ABCD gấp 4 lần diện tích tam giác AEB nên diện tích hình vuông ABCD là: .4 = 2 (m2).
Vậy diện tích hình vuông ABCD là 2 m2.
b) Do là độ dài đường chéo của hình vuông có cạnh bằng 1, mà hình vuông AEBF có cạnh bằng 1 m nên đường chéo AB là m.
Vậy độ dài đường chéo AB là m.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
a) Đọc các số sau:
b) Viết các số sau: Căn bậc hai số học của 39; căn bậc hai số học của ; căn bậc hai số học của .
a) Đọc các số sau:
b) Viết các số sau: Căn bậc hai số học của 39; căn bậc hai số học của ; căn bậc hai số học của .
Xem đáp án »
13/07/2024
5,580
Câu 2:
Khẳng định “Mỗi số vô tỉ đều không thể là số hữu tỉ” là đúng hay sai? Vì sao?
Khẳng định “Mỗi số vô tỉ đều không thể là số hữu tỉ” là đúng hay sai? Vì sao?
Xem đáp án »
13/07/2024
3,782
Câu 5:
Ta có thể tính được giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số dương bằng máy tính cầm tay. Chẳng hạn, để tính , ta sử dụng nút dấu căn bậc hai số học và làm như sau:
Ta có thể tính được giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số dương bằng máy tính cầm tay. Chẳng hạn, để tính , ta sử dụng nút dấu căn bậc hai số học và làm như sau:
Xem đáp án »
13/07/2024
1,549
Câu 6:
Chứng tỏ rằng:
a) Số 0,8 là căn bậc hai số học của 0,64;
b) Số –11 không phải căn bậc hai số học của 121.
c) Số 1,4 là căn bậc hai số học của 1,96 nhưng –1,4 không phải căn bậc hai số học của 1,96.
Chứng tỏ rằng:
a) Số 0,8 là căn bậc hai số học của 0,64;
b) Số –11 không phải căn bậc hai số học của 121.
c) Số 1,4 là căn bậc hai số học của 1,96 nhưng –1,4 không phải căn bậc hai số học của 1,96.
Xem đáp án »
13/07/2024
1,128
về câu hỏi!