Cho hình chóp S.ABCD có các cạnh bên SA, SB, SC tạo với đáy các góc bằng nhau và đều bằng . Biết , khoảng cách từ A đến mặt phẳng (SBC) bằng
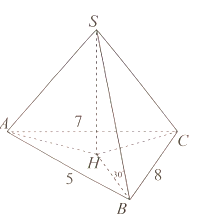
Cho hình chóp S.ABCD có các cạnh bên SA, SB, SC tạo với đáy các góc bằng nhau và đều bằng . Biết , khoảng cách từ A đến mặt phẳng (SBC) bằng

Quảng cáo
Trả lời:
Đáp án B
Gọi H là chân đường vuông góc kẻ từ S đến mặt phẳng (ABC)
Khi đó từ giả thiết ta có
Suy ra (gn-cgv)
Suy ra hay H là tâm đường tròn ngoại tiếp .
Tam giác ABC có
Theo công thức Hê-rông thì diện tích tam giác ABC là
Lại có (với R là bán kính đường tròn ngoại tiếp ).
Hay .
Xét tam giác SHA vuông tại H có .
Thể tích khối chóp S.ABC là .
Lại có vuông tại H nên
Xét tam giác SBC có suy ra
Từ đó .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án A
Xét , ta có hàm số đồng biến trên .
Lời giải
Đáp án C
Ta có
(*)
Xét hàm số có là hàm số đồng biến trên .
Phương trình (*) suy ra
(vì chỉ có hai nghiệm phân biệt nên ).
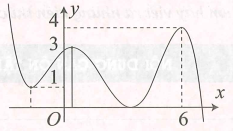
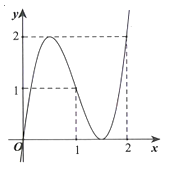
+ Vì nên từ đồ thị hàm số ta thấy phương trình có một nghiệm duy nhất.
Từ yêu cầu bài toán suy ra phương trình có hai nghiệm phân biệt.
+ Vì nên từ đồ thị hàm số
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
D. -5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.