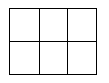
Bé Minh có một bảng hình chữ nhật gồm 6 hình vuông đơn vị, cố định không xoay như hình vẽ. Bé muốn dùng 3 màu để tô tất cả các cạnh của các hình vuông đơn vị, mỗi cạnh tô một lần sao cho hình vuông đơn vị được tô bởi đúng 2 màu, trong đó mỗi màu tô đúng hai cạnh. Hỏi bé Minh có tất cả bao nhiêu cách tô màu bảng?
A. 139968.
B. 4374.
C. 576.
D. 15552.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn D
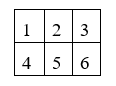
+ Tô màu ô vuông số 2: có cách chọn 2 trong 3 màu, có cách tô 2 màu đó lên 4 cạnh. Vậy có = 18cách.
+ Tô màu ô vuông số 1,5,3: có cách chọn màu còn lại, có cách tô màu còn lại lên 3 cạnh còn lại của 1 hình vuông. Vậy có ( = cách
+ Tô màu ô vuông số 4,6: Mỗi 1 hình vuông có 2 cách tô màu. Vậy có = 4cách.
Vậy có 18..4 = 15552 cách thỏa mãn.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 43200
B. 94536
C. 55012
D. 35684
Lời giải
Chọn A
Xếp 6 học sinh có 6! cách xếp.
Giữa 6 học sinh có 5 khoảng trống.
Xếp 3 thầy giáo A, B, C vào 5 khoảng trống trên có: cách.
Vậy số cách xếp thỏa mãn yêu cầu là: 6!. = 43200 cách.
Lời giải
Chọn C.
Gọi số cần tìm là n = .
Ta có a có 9 cách chọn. Số cách xếp các số còn lại vào vị trí b, c là .
Vậy số các số cần tìm là 9. = 648.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 12
B. 3
C. 36
D. 72
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. n(n+1)(n+2) = 120
B. n(n+1)(n+2) = 720
C. n(n-1)(n-2) = 120
D. n(n-1)(n-2) = 720
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập