Câu hỏi:
12/07/2024 364
Tính chất của các số
a) Quan sát ba dòng đầu, hoàn thành tiếp hai dòng cuối theo mẫu:
(a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 = ...
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5 = ...
Nhận xét rằng các hệ số khai triển của hai số hạng cách đều số hạng đầu và số hạng cuối luôn bằng nhau. Hãy so sánh, chẳng hạn, và , và . Từ đó hãy dự đoán hệ thức giữa và (0 ≤ k ≤ n).
b) Dựa vào kết quả của HĐ3a, ta có thể viết những hàng đầu của tam giác Pascal dưới dạng:
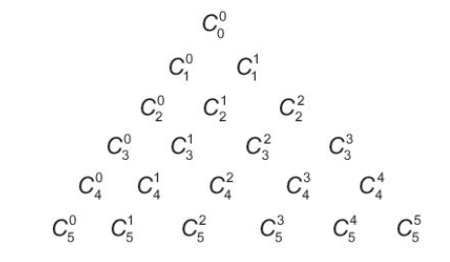
(a + b)1
(a + b)2
(a + b)3
(a + b)4
(a + b)5
Từ tính chất của tam giác Pascal, hãy so sánh và và Từ đó hãy dự đoán hệ thức giữa và
Tính chất của các số
a) Quan sát ba dòng đầu, hoàn thành tiếp hai dòng cuối theo mẫu:
(a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 = ...
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5 = ...
Nhận xét rằng các hệ số khai triển của hai số hạng cách đều số hạng đầu và số hạng cuối luôn bằng nhau. Hãy so sánh, chẳng hạn, và , và . Từ đó hãy dự đoán hệ thức giữa và (0 ≤ k ≤ n).
b) Dựa vào kết quả của HĐ3a, ta có thể viết những hàng đầu của tam giác Pascal dưới dạng:
(a + b)1
(a + b)2
(a + b)3
(a + b)4
(a + b)5
Từ tính chất của tam giác Pascal, hãy so sánh và và Từ đó hãy dự đoán hệ thức giữa và
Câu hỏi trong đề:
Bài tập Nhị thức newton có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 = a4 + a3b + a2b2 + ab3 + b4.
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
= a5 + a4b + a3b2 + a2b3 + ab4 + b5.
Ta thấy = , = ,...
Dự đoán: = .
b) Ta thấy = =
Dự đoán: =
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Tìm hệ số của x7 trong khai triền thành đa thức của (2 – 3x)10.
Tìm hệ số của x7 trong khai triền thành đa thức của (2 – 3x)10.
Xem đáp án »
12/07/2024
4,650
Câu 3:
(Số các tập con của tập hợp có n phần tử)
a) Viết khai triển nhị thức Newton của (1 + x)n.
b) Cho x = 1 trong khai triển ở câu a), viết đẳng thức nhận được. Giải thích ý nghĩa của đẳng thức này với lưu ý rằng (0 < k < n) chính là số tập con gồm k phần tử của một tập hợp có n phần tử.
c) Tương tự, cho x = –1 trong khai triển ở câu a), viết đẳng thức nhận được. Giải thích ý nghĩa của đẳng thức này.
(Số các tập con của tập hợp có n phần tử)
a) Viết khai triển nhị thức Newton của (1 + x)n.
b) Cho x = 1 trong khai triển ở câu a), viết đẳng thức nhận được. Giải thích ý nghĩa của đẳng thức này với lưu ý rằng (0 < k < n) chính là số tập con gồm k phần tử của một tập hợp có n phần tử.
c) Tương tự, cho x = –1 trong khai triển ở câu a), viết đẳng thức nhận được. Giải thích ý nghĩa của đẳng thức này.
Xem đáp án »
12/07/2024
4,373
Câu 6:
Từ khai triển biểu thức (3x – 5)4 thành đa thức, hãy tính tổng các hệ số của đa thức nhận được.
Từ khai triển biểu thức (3x – 5)4 thành đa thức, hãy tính tổng các hệ số của đa thức nhận được.
Xem đáp án »
12/07/2024
3,529
về câu hỏi!