Câu hỏi:

17/06/2022 10,937

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D cạnh bên SA vuông góc với mặt đáy. Biết AB=2AD=2DC=2a góc giữa hai mặt phẳng (SAB) và (SBC) là 60 độ . Độ dài cạnh SA là:

a \sqrt{2} .

2 a \sqrt{3} .

3 a \sqrt{2} .

a \sqrt{3} .

Xem lời giải

Câu hỏi trong đề: Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án A

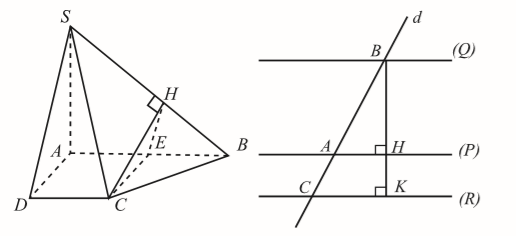
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D cạnh bên SA vuông góc với mặt đáy. Biết AB=2AD=2DC=2a góc giữa hai mặt phẳng (SAB) và (SBC) là 60 độ . Độ dài cạnh SA là: (ảnh 1)

Gọi E là trung điểm của AB. Ta dễ dàng chứng minh được ABCE là hình vuông

$\Rightarrow {\begin{cases} C E ⊥ A B \\ C E ⊥ S A \end{cases} \Rightarrow C E ⊥ (S A B) \Rightarrow C E ⊥ S B$

Trong (SAB) kẻ $H E ⊥ S B$ ta có: ${\begin{cases} S B ⊥ E H \\ S B ⊥ C E \end{cases} \Rightarrow S B ⊥ (C H E) \Rightarrow S B ⊥ C H$

${\begin{cases} (S A B) \cap (S B C) = S B \\ (S A B) \supset E H ⊥ S B \\ (S A C) \supset C H ⊥ S B \end{cases} \Rightarrow \hat{((S A B), (S B C))} = \hat{(E H, C H)} = \hat{C H E} = 60^{o}$ Xét tam giác vuông CEH có $E H = C E . \cot 60^{o} = \frac{a}{\sqrt{3}} .$

Ta có $Δ S A B ~ Δ E H G (g . g) \Rightarrow \frac{S A}{E H} = \frac{S B}{B E} \Rightarrow S A = \frac{E H . S B}{B E} = \frac{\frac{a}{\sqrt{3}} . \sqrt{S A^{2} + 4 a^{2}}}{a}$

$\Leftrightarrow \sqrt{3} S A = \sqrt{S A^{2} + 4 a^{2} \Leftrightarrow} 3 S A^{2} = S A^{2} + 4 a^{2} \Leftrightarrow S A^{2} = 2 a^{2} \Leftrightarrow S A = a \sqrt{2}$

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho khối chóp SABCD có đáy là hình vuông cạnh $\frac{a}{\sqrt{2}}, Δ S A C$ vuông tại S và nằm trong mặt phẳng vuông góc với đáy, cạnh bên SA tạo với đáy góc $60^{o}$ . Tính thể tích V của khối chóp SABCD.

V = \frac{a^{3} \sqrt{3}}{24} .

V = \frac{a^{3} \sqrt{3}}{12} .

V = \frac{a^{3} \sqrt{6}}{24} .

V = \frac{a^{3} \sqrt{2}}{24} .

Lời giải

Đáp án A

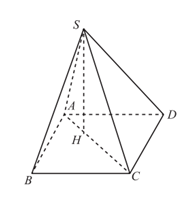
Cho khối chóp SABCD có đáy là hình vuông cạnh a/ căn2, tam giác SAC vuông tại S và nằm trong mặt phẳng vuông góc với đáy, cạnh bên SA tạo với đáy góc 60 độ . Tính thể tích V của khối chóp SABCD. (ảnh 1)

Gọi H là hình chiếu của S trên AC.

Ta có ${\begin{cases} (S A C) \cap (A B C D) = A C \\ (S A C) \supset S H ⊥ A C \end{cases} \Rightarrow S H ⊥ (A B C D)$

Ta có: $∠ (S A, (A B C D)) = ∠ (S A, A H) = ∠ (S A, A C) = ∠ S A C$

Ta có: $∠ A C = A B \sqrt{2} = \frac{a \sqrt{2}}{2} . \sqrt{2} = a$

Xét $Δ S A C$ vuông tại S ta có: ${\begin{cases} S A = A C . c o s 60^{o} = \frac{a}{2} \\ S C = A C . \sin 60^{o} = \frac{a \sqrt{3}}{2} \end{cases}$

Áp dụng hệ thức lượng cho $Δ S A C$ vuông tại S và có đường cao SH ta có:

$S H = \frac{S A . S C}{A C} = \frac{\frac{a}{2} . \frac{a \sqrt{3}}{2}}{a} = \frac{a \sqrt{3}}{4}$

$\Rightarrow V_{S . A B C D} = \frac{1}{3} S A . S_{A B C D} = \frac{1}{3} . \frac{a \sqrt{3}}{4} . \frac{a^{2}}{2} = \frac{a^{3} \sqrt{3}}{24}$ $\Rightarrow V_{S . A B C D} = \frac{1}{3} S A . S_{A B C D} = \frac{1}{3} . \frac{a \sqrt{3}}{4} . \frac{a^{2}}{2} = \frac{a^{3} \sqrt{3}}{24}$

Câu 2

Trong không gian với hệ tọa độ Oxyz, cho $A (- 3; 0; 0); B (0; 0; 3); C (0; - 3; 0)$ và mặt phẳng $(P) : x + y + z - 3 = 0.$ Tìm trên (P) điểm M sao cho $| \vec{M A} + \vec{M B} - \vec{M C} |$ nhỏ nhất

M (3; 3; - 3) .

M (3; - 3; 3) .

M (- 3; 3; 3) .

M (- 3; - 3; 3) .

Lời giải

Đáp án C

Gọi điểm $I (a, b, c)$ thỏa mãn $\vec{I A} + \vec{I B} - \vec{I C} = \vec{0}$

Ta có: ${\begin{cases} \vec{I A} = (- 3 - a; - b; - c) \\ \vec{I B} = (- a; - b; 3 - c) \\ \vec{I C} = (- a; - 3 - b; - c) \end{cases} \Rightarrow \vec{I A} + \vec{I B} - \vec{I C} = (- 3 - a; 3 - b; 3 - c) = \vec{0}$

$\Leftrightarrow {\begin{cases} - 3 - a = 0 \\ 3 - b = 0 \\ 3 - c = 0 \end{cases} \Leftrightarrow {\begin{cases} a = - 3 \\ b = 3 \\ c = 3 \end{cases} \Leftrightarrow I (- 3; 3; 3)$

Ta có $| \vec{M A} + \vec{M B} - \vec{M C} | = | \vec{M I} + \vec{I A} + \vec{M I} + \vec{I B} - \vec{M I} - \vec{I C} | = | \vec{M I} + (\vec{I A} + \vec{I B} - \vec{I C}) | = | \vec{M I} | = M I$

Do đó nhỏ nhất khi và chỉ khi MI nhỏ nhất là hình chiếu của I trên (P)

Ta thấy $- 3 + 3 + 3 - 3 = 0 \Rightarrow I \in (P)$

Nên hình chiếu của I trên (P) là chính nó

Do đó $M \equiv I \Rightarrow M (- 3; 3; 3)$

Câu 3

Cho hình chóp S.ABCD có $S C = x (0 < x < a \sqrt{3}),$ các cạnh còn lại đều bằng a. Biết rằng thể tích khối chóp S.ABCD lớn nhất khi và chỉ khi $x = \frac{a \sqrt{m}}{n} (m, n \in ℕ^{*})$ . Mệnh đề nào sau đây đúng?

A. $m + 2 n = 10.$

2 m^{2} - 3 m < 15.

m^{2} - n = 30.

4 m - n^{2} = - 20.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong không gian với hệ trục tọa độ Oxyz cho $\vec{a} = (1; - 2; 3)$ và $\vec{b} = (2; - 1; - 1)$ . Khẳng định nào sau đây đúng?

A. Vecto

\vec{a}

không vuông góc với

\vec{b}

B. Vecto

\vec{a}

cùng phương với

\vec{b}

| \vec{a} | = \sqrt{14} .

[\vec{a}; \vec{b}] = (- 5; - 7; - 3)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm B( 2;1;-3) đồng thời vuông góc với hai mặt phẳng (Q): x+y+3z=0 , (R): 2x-y+z=0 là:

4 x + 5 y - 3 z + 22 = 0.

B. $4 x + 5 y - 3 z + 22 = 0.$

2 x + y - 3 z - 14 = 0.

4 x + 5 y - 3 z - 22 = 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số $y = f (x)$ thỏa mãn ${[f' (x)]}^{2} + f (x) . f'' (x) = x^{3} - 2 x \forall x \in ℝ$ và $f (0) = f' (0) = 2.$ Tính giá trị của $T = f^{2} (2)$

\frac{268}{15} .

\frac{160}{15} .

\frac{268}{30} .

\frac{4}{15} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Cho khối chóp SABCD có đáy là hình vuông cạnh $\frac{a}{\sqrt{2}}, Δ S A C$ vuông tại S và nằm trong mặt phẳng vuông góc với đáy, cạnh bên SA tạo với đáy góc $60^{o}$ . Tính thể tích V của khối chóp SABCD.

Trong không gian với hệ tọa độ Oxyz, cho $A (- 3; 0; 0); B (0; 0; 3); C (0; - 3; 0)$ và mặt phẳng $(P) : x + y + z - 3 = 0.$ Tìm trên (P) điểm M sao cho $| \vec{M A} + \vec{M B} - \vec{M C} |$ nhỏ nhất

Cho hình chóp S.ABCD có $S C = x (0 < x < a \sqrt{3}),$ các cạnh còn lại đều bằng a. Biết rằng thể tích khối chóp S.ABCD lớn nhất khi và chỉ khi $x = \frac{a \sqrt{m}}{n} (m, n \in ℕ^{*})$ . Mệnh đề nào sau đây đúng?

Trong không gian với hệ trục tọa độ Oxyz cho $\vec{a} = (1; - 2; 3)$ và $\vec{b} = (2; - 1; - 1)$ . Khẳng định nào sau đây đúng?

Cho hàm số $y = f (x)$ thỏa mãn ${[f' (x)]}^{2} + f (x) . f'' (x) = x^{3} - 2 x \forall x \in ℝ$ và $f (0) = f' (0) = 2.$ Tính giá trị của $T = f^{2} (2)$