Câu hỏi:
04/07/2022 2,943
Các nhà thiên văn tính được thời gian để Trái Đất quay một vòng quanh Mặt Trời là 365 ngày \( \pm \frac{1}{4}\) ngày. Bạn Hùng tính thời gian đi bộ một vòng quanh sân vận động của trường khoảng 15 phút ± 1 phút. Trong hai phép đo trên, phép đo nào chính xác hơn?
Câu hỏi trong đề: Bài tập Số gần đúng. Sai số có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Phép đo của các nhà thiên văn có sai số tuyệt đối không vượt quá \(\frac{1}{4}\) ngày, có nghĩa là không vượt quá 360 phút. Phép đo của Hùng có sai số tuyệt đối không quá 1 phút. Nếu chỉ so sánh 360 phút và 1 phút thì có thể dẫn đến hiểu rằng phép đo của bạn Hùng chính xác hơn phép đo của các nhà thiên văn. Tuy nhiên, \(\frac{1}{4}\) ngày hay 360 phút là độ chính xác của phép đo một chuyển động trong 365 ngày, còn 1 phút là độ chính xác của phép đo một chuyển động trong 15 phút. So sánh hai tỉ số \(\frac{{\frac{1}{4}}}{{365}} = \frac{1}{{1460}} = 0,0006849...\) và \(\frac{1}{{15}} = 0,0666....\), ta thấy rằng phép đo của các nhà thiên văn chính xác hơn nhiều.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Ta mô phỏng màn hình ti vi có hình chữ nhật ABCD như sau:
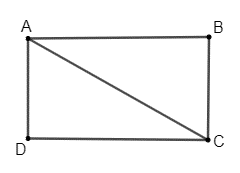
Ta có: AC = 32 in, AB là chiều dài, BC là chiều rộng với AB : BC = 16 : 9.
Gọi chiều dài của ti vi là x (in, x > 0) hay AB = x, khi đó chiều rộng của ti vi là \(BC = \frac{9}{{16}}x\).
Sử dụng định lí Pythagore, ta có phương trình: \({x^2} + {\left( {\frac{9}{{16}}x} \right)^2} = {32^2}\) (*).
Giải phương trình (*), ta có:
(*) \( \Leftrightarrow {x^2} + \frac{{81}}{{256}}{x^2} = 1024\)\( \Leftrightarrow \frac{{337}}{{256}}{x^2} = 1024 \Leftrightarrow {x^2} = \frac{{262144}}{{337}}\)
Do x > 0 nên x = \(\frac{{512}}{{\sqrt {337} }}\).
Vậy chiều dài của chiếc ti vi là \(\frac{{512}}{{\sqrt {337} }} = 27,89041719...\) (in).
Quy tròn số \(\frac{{512}}{{\sqrt {337} }}\) đến hàng phần trăm được 27,89.
Ta có độ chính xác d = 0,005 (nửa đơn vị hàng quy tròn).
Vậy sai số tương đối \({\delta _a} \le \frac{{0,005}}{{27,89}} \approx 0,02\% \).
Lời giải
Hướng dẫn giải
Do 0,001 < d = 0,009 < 0,01 nên hàng thấp nhất mà d nhỏ hơn một đơn vị của hàng đó là hàng phần trăm. Vì thế, ta quy tròn số 30,2376 đến hàng phần trăm theo quy tắc quy tròn.
Vậy số quy tròn của 30,2376 là 30,24.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
10 Bài tập Tìm hệ số, số hạng trong khai triển nhị thức Newton (có lời giải)
-
50 câu trắc nghiệm Thống kê cơ bản (phần 1)