Câu hỏi:
08/07/2022 6,676
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 4sin3 x + 9cos2 x + 6sin x -10. Giá trị của tích M.m bằng
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 4sin3 x + 9cos2 x + 6sin x -10. Giá trị của tích M.m bằng
Đáp án chính xác
Câu hỏi trong đề:
Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
y = 4sin3 x + 9cos2 x + 6sin x - 10
= 4sin3 x + (9cos2 x - 9) + 6sin x - 1
= 4sin3 x - 9sin2 x + 6sin x - 1
Đặt f (t) = 4t3 - 9t2 + 6t - 1 với t = sin x Î [-1; 1]
(12t2 -12t) - (6t - 6) = 0
12t.(t - 1) - 6(t - 1) = 0
6(2t -1).(t - 1) = 0
Xét bảng biến thiên của hàm số f (t) = 4t3 - 9t2 + 6t - 1 trên đoạn [-1; 1]
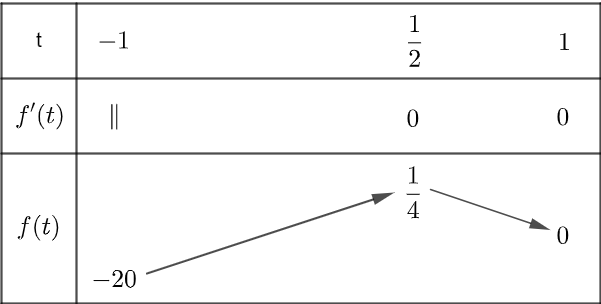
Dựa vào bảng biến thiên, suy ra
Do đó
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian Oxyz, cho hai điểm A(-1; 0; 2), B(3; 2; -2). Biết tập hợp các điểm M thỏa mãn MA2 + MB2 = 30 là một mặt cầu. Bán kính mặt cầu đó bằng
Trong không gian Oxyz, cho hai điểm A(-1; 0; 2), B(3; 2; -2). Biết tập hợp các điểm M thỏa mãn MA2 + MB2 = 30 là một mặt cầu. Bán kính mặt cầu đó bằng
Xem đáp án »
10/07/2022
6,899
Câu 3:
Cho log2 3 = a. Giá trị của biểu thức P = log6 12 tính theo a bằng
Xem đáp án »
07/07/2022
6,652
Câu 6:
Trong không gian tọa độ Oxyz, cho hai điểm A(-1; 2; 0), B(-3; 4; 2). Phương trình mặt cầu đường kính AB là
Xem đáp án »
08/07/2022
5,710
Bình luận
🔥 Đề thi HOT:
-
53 câu Bài tập về Tính đơn điệu của hàm số có lời giải (P1)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
-
200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P1)
-
120 câu Bài tập Cực trị hàm số cơ bản, nâng cao có lời giải (P1)
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
về câu hỏi!