Biết rằng \[\int\limits_2^4 {\frac{{{x^3} + 2}}{{{x^2} + x}}dx} = a + b\ln 2 + c\ln 3 + d\ln 5,\] với \[a,{\rm{ }}b,{\rm{ }}c,{\rm{ }}d \in \mathbb{Z}.\] Tính giá trị của biểu thức \[S = a + b + c + d.\]
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Đáp án A
Phân tích \(\frac{{{x^3} + 2}}{{{x^2} + x}} = \frac{{x\left( {{x^2} + x} \right) - \left( {{x^2} + x} \right) + x + 2}}{{{x^2} + x}} = x - 1 + \frac{{x + 2}}{{x\left( {x + 1} \right)}} = x - 1 + \frac{m}{x} + \frac{n}{{x + 1}}\)
\( \Rightarrow x + 2 = m\left( {x + 1} \right) + nx,\) cho \(\left\{ \begin{array}{l}x = 0 \Rightarrow m = 2\\x = - 1 \Rightarrow n = - 1\end{array} \right. \Rightarrow \int\limits_2^4 {\frac{{{x^3} + 2}}{{{x^2} + x}}dx} = \int\limits_2^4 {\left( {x - 1 + \frac{2}{x} - \frac{1}{{x + 1}}} \right)dx} \)
\( \Rightarrow I = \left. {\left( {\frac{{{x^2}}}{2} - x + 2\ln \left| x \right| - \ln \left| {x + 1} \right|} \right)} \right|_2^4 = \left( {4 + 2\ln 4 - \ln 5} \right) - \left( {2\ln 2 - \ln 3} \right)\)
\( = 4 + 2\ln 2 + \ln 3 - \ln 5 \Rightarrow a = 4,{\rm{ }}b = 2,{\rm{ }}c = 1,{\rm{ }}d = - 1 \Rightarrow S = 6.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án C
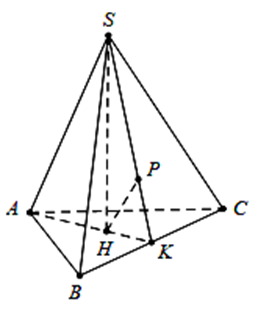
Kẻ \(SH \bot \left( {ABC} \right)\), gọi \(K = AH \cap BC\).
Kẻ \(HP \bot {\rm{S}}K \Rightarrow d\left( {A;(SBC)} \right) = \frac{3}{2}d\left( {H;(SBC)} \right) = \frac{3}{2}HP = d\).
Ta có \(\frac{1}{{H{P^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{K^2}}}\). Cạnh \(HK = \frac{{AB}}{{2\sqrt 3 }} = \frac{a}{{2\sqrt 3 }}\)
\(S{H^2} = S{A^2} - A{H^2} = 4{{\rm{a}}^2} - {\left( {\frac{{AB}}{{\sqrt 3 }}} \right)^2} = \frac{{11{{\rm{a}}^2}}}{3}\)
\( \Rightarrow HP = a\sqrt {\frac{{11}}{{135}}} \Rightarrow d\left( {A;(SBC)} \right) = \frac{{a\sqrt {165} }}{{15}}\).
Câu 2
Lời giải
Đáp án D
Ta có \(\int\limits_0^2 {f\left( x \right)d{\rm{x}}} = \int\limits_0^1 {f\left( x \right)d{\rm{x}}} + \int\limits_1^2 {f\left( x \right)d{\rm{x}}} = - 1\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.