Cho ba số phức \[{z_1},{\rm{ }}{z_2},{\rm{ }}{z_3}\] thỏa mãn \[\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = 1\]; \[\left| {{z_1} - {z_2}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2}\] và \[z_1^2 = {z_2}{z_3}.\] Tính giá trị của \[\left| {{z_2} - {z_3}} \right| - \left| {{z_3} - {z_1}} \right|\].
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Đáp án D
Gọi M, N, P lần lượt là các điểm biểu diễn các số phức \({z_1},{z_2},{z_3}\).
Suy ra M, N, P thuộc đường tròn \(\left( {O;1} \right)\).
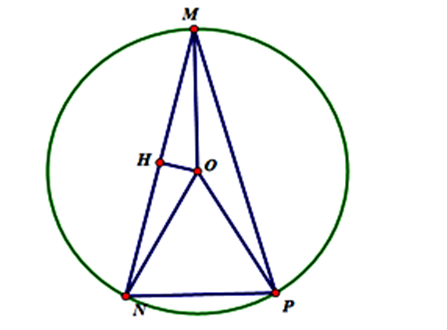
Ta có \(MN = \left| {{z_1} - {z_2}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2}\).
Kẻ \(OH \bot MN \Rightarrow MH = \frac{{MN}}{2} = \frac{{\sqrt 6 + \sqrt 2 }}{4} \Rightarrow \cos \widehat {OMN} = \frac{{MN}}{{OM}} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\)
\( \Rightarrow \widehat {OMN} = {15^0} \Rightarrow \widehat {MON} = {150^0}\)
Ta có \(\left| {{z_3} - {z_1}} \right| = \left| {{z_1}} \right|.\left| {{z_3} - {z_1}} \right| = \left| {{z_3}{z_1} - z_1^2} \right| = \left| {{z_3}{z_1} - {z_3}{z_2}} \right| = \left| {{z_3}} \right|.\left| {{z_1} - {z_2}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2}\)
\( \Rightarrow MP = \left| {{z_3} - {z_1}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2} \Rightarrow MN = MP = \frac{{\sqrt 6 + \sqrt 2 }}{2}.\)
Tương tự như trên \( \Rightarrow \widehat {MOP} = {150^0} \Rightarrow \widehat {NOP} = {360^0} - \left( {{{150}^0} + {{150}^0}} \right) = {60^0}\)
\( \Rightarrow \Delta NOP\) đều \( \Rightarrow NP = 1\)
\( \Rightarrow \left| {{z_2} - {z_3}} \right| = NP = 1 \Rightarrow \left| {{z_2} - {z_3}} \right| - \left| {{z_3} - {z_1}} \right| = 1 - \frac{{\sqrt 6 + \sqrt 2 }}{2} = \frac{{2 - \sqrt 6 - \sqrt 2 }}{2}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án C
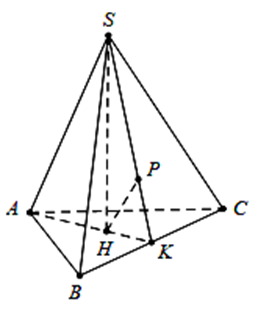
Kẻ \(SH \bot \left( {ABC} \right)\), gọi \(K = AH \cap BC\).
Kẻ \(HP \bot {\rm{S}}K \Rightarrow d\left( {A;(SBC)} \right) = \frac{3}{2}d\left( {H;(SBC)} \right) = \frac{3}{2}HP = d\).
Ta có \(\frac{1}{{H{P^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{K^2}}}\). Cạnh \(HK = \frac{{AB}}{{2\sqrt 3 }} = \frac{a}{{2\sqrt 3 }}\)
\(S{H^2} = S{A^2} - A{H^2} = 4{{\rm{a}}^2} - {\left( {\frac{{AB}}{{\sqrt 3 }}} \right)^2} = \frac{{11{{\rm{a}}^2}}}{3}\)
\( \Rightarrow HP = a\sqrt {\frac{{11}}{{135}}} \Rightarrow d\left( {A;(SBC)} \right) = \frac{{a\sqrt {165} }}{{15}}\).
Câu 2
Lời giải
Đáp án D
Ta có \(\int\limits_0^2 {f\left( x \right)d{\rm{x}}} = \int\limits_0^1 {f\left( x \right)d{\rm{x}}} + \int\limits_1^2 {f\left( x \right)d{\rm{x}}} = - 1\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.