Bộ 5 đề thi cuối kì 2 Toán 6 Kết nối tri thức (Tự luận) có đáp án - Đề 2

a) \(\frac{{ - 5}}{8} \cdot \frac{{ - 12}}{{29}} \cdot \frac{8}{{ - 10}} \cdot 2,9\)

\( = \frac{{ - 5}}{8} \cdot \frac{{ - 6 \cdot 2}}{{29}} \cdot \frac{8}{{ - 5 \cdot 2}} \cdot \frac{{29}}{{10}}\)

\( = \frac{{ - 6}}{{10}} =  - \frac{3}{5}.\)

a) \(x:\frac{8}{5} = \frac{5}{2}\)

 \(x = \frac{5}{2} \cdot \frac{8}{5}\)

 \(x = 4\)

Chiều rộng của khu vườn là: \(4,5:15\% = 30{\rm{\;(m)}}{\rm{.}}\)

Diện tích của khu vườn là: \(50 \cdot 30 = 1500{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

Diện tích đào ao là: \(360:\frac{6}{7} = 420{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

Diện tích trồng rau là: \(65\% \cdot \left( {1500 - 420} \right) = 702{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

Diện tích trồng hoa là: \(1500 - 420 - 702 = 378{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

1) a)

Vì hai điểm \(A,\,\,B\) cùng nằm trên tia \(Oy\) và \(OA < OB\) (do \(3{\rm{\;cm}} < 5{\rm{\;cm}})\) nên điểm \(A\) nằm giữa hai điểm \(O,\,\,B.\)

b) Vì điểm \(A\) nằm giữa hai điểm \(O,\,\,B\) nên ta có: \(OA + AB = OB\)

Suy ra \(AB = OB - OA = 5 - 3 = 2{\rm{\;(cm)}}{\rm{.}}\)

c)

Vì điểm \(A\) thuộc tia \(Oy,\) điểm \(C\) thuộc tia \[Ox\] mà hai tia \(Ox\) và \(Oy\) đối nhau nên điểm \(O\) nằm giữa hai điểm \(A\) và \(C\)

Do đó \(OC + OA = AC\)

Suy ra \(OC = AC - OA = 6 - 3 = 3{\rm{\;(cm)}}{\rm{.}}\)

Ta có nên điểm \(O\) nằm giữa hai điểm \(A,\,\,C\) và \(OA = OC\,\,\left( { = 3{\rm{\;cm}}} \right)\) nên điểm \(O\) là trung điểm của đoạn thẳng \(AC.\)

2) a) Góc vuông có số đo bằng \(90^\circ ;\) góc bẹt có số đo bằng \(180^\circ .\)

b) Ta có: \(0^\circ < 30^\circ < 45^\circ < 90^\circ < 120^\circ < 135^\circ < 180^\circ \)

Do đó \[0^\circ < \widehat {A\,} < \widehat {D\,} < \widehat {B\,} = 90^\circ < \widehat {E\,} < \widehat {C\,} < 180^\circ \]

Như vậy, trong các góc đã cho có 2 góc nhọn là \(\widehat {A\,},\,\,\widehat {D\,}\) và có 2 góc tù là \(\widehat {E\,},\,\,\widehat {C\,}.\)

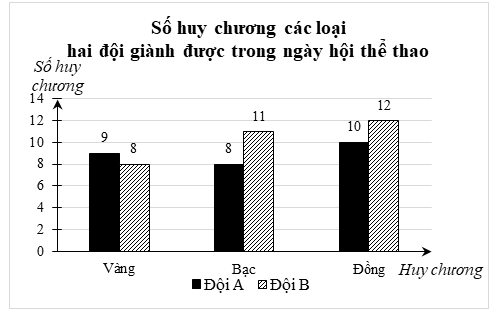
1) a) Biểu đồ cột kép trên cho biết về số huy chương các loại (Vàng, Bạc, Đồng) mà đội A và đội B giành được trong ngày hội thể thao.

b) Tổng số huy chương các loại của đội A là: \(9 + 8 + 10 = 27\) (huy chương).

Tổng số huy chương các loại của đội B là: \(8 + 11 + 12 = 31\) (huy chương).

c) Tổng số điểm đội A đạt được là: \(9 \cdot 5 + 8 \cdot 4 + 10 \cdot 3 = 107\) (điểm).

Tổng số điểm đội B đạt được là: \(8 \cdot 5 + 11 \cdot 4 + 12 \cdot 3 = 120\) (điểm).

Như vậy, đội B đạt được tổng số điểm nhiều hơn, và nhiều hơn \(120 - 107 = 13\) điểm.

2) Quan sát bảng kết quả, ta thấy rằng bạn An đổ xúc xắc được số 6 chấm trước bạn Bình nên bạn An được cắm ngựa đi trước.

Có 5 lần đổ xúc xắc mà số chấm trên xúc xắc của Bình hơn của An 1 đơn vị là: lần 1, lần 3, lần 6, lần 9, lần 10.

Như vậy, xác suất của sự kiện số chấm trên xúc xắc của Bình hơn của An 1 đơn vị là: \(\frac{5}{{10}} = \frac{1}{2}.\)