Bộ 5 đề thi cuối kì 2 Toán 6 Kết nối tri thức (Tự luận) có đáp án - Đề 3

a) \(\frac{1}{5} + \frac{{ - 5}}{{19}} + \frac{4}{5} + \frac{{ - 14}}{{19}}\)

\( = \left( {\frac{1}{5} + \frac{4}{5}} \right) + \left( {\frac{{ - 5}}{{19}} + \frac{{ - 14}}{{19}}} \right)\)

\( = \frac{5}{5} + \frac{{ - 19}}{{19}}\)

\( = 1 + \left( { - 1} \right) = 0.\)

a) \(\frac{1}{6} - x = \frac{{ - 1}}{{42}}\)

\(x = \frac{1}{6} - \frac{{ - 1}}{{42}}\)

\(x = \frac{7}{{42}} + \frac{1}{{42}}\)

\(x = \frac{8}{{42}}\)

\(x = \frac{4}{{21}}\)

a) Số cam còn lại sau buổi sáng là: \(100\% - 60\% = 40\% \) (tổng số cam).

Số cam buổi chiều bán được là \(\frac{{13}}{{18}} \cdot 40\% = \frac{{13}}{{45}}\) (tổng số cam).

Số cam còn lại sau cả một ngày bán là: \(40\% - \frac{{13}}{{45}} = \frac{1}{9}\) (tổng số cam).

\(20\) quả cam chiếm \(\frac{1}{9}\) tổng số cam nên số cam người đó mang đi bán là: \(20:\frac{1}{9} = 180\) (quả).

b) Số quả cam bán trong buổi sáng là: \(180 \cdot 60\% = 108\) (quả).

Số quả cam bán trong buổi chiều là: \(180 - 108 - 20 = 52\) (quả).

Tổng số cam bán được trong ngày là: \(108 + 52 = 160\) (quả).

Tỉ số phần trăm số cam người đó bán được buổi sáng so với tổng số cam bán được trong ngày là \(\frac{{108}}{{160}} \cdot 100\% = 67,5\% .\)

1)

a) Vì điểm \(A\) thuộc tia \[Ox\] và tia \(M\) thuộc tia đối của tia \(Ox\) nên điểm \(O\) nằm giữa hai điểm \(A,\,\,M.\)

Lại có \(OA = OM\) nên điểm \(O\) là trung điểm của đoạn thẳng \(AM.\)

b) ⦁ Ta có \(OM = OA = 4{\rm{\;cm}}\) và \(OB = 8{\rm{\;cm}}\) nên \(OM < OB\)

Mà hai điểm \(B\) và \(M\) nằm trên tia đối của tia \(Ox\) nên điểm \(M\) nằm giữa hai điểm \(O\) và \(B\)

Do đó \(OB = BM + OM\)

Suy ra \(BM = OB - OM = 8 - 4 = 4{\rm{\;(cm)}}{\rm{.}}\)

⦁ Vì điểm \(A\) thuộc tia \[Ox\] và tia \(B\) thuộc tia đối của tia \(Ox\) nên điểm \(O\) nằm giữa hai điểm \(A\) và \(B\)

Do đó \(AB = BO + OA = 8 + 4 = 12{\rm{\;(cm)}}{\rm{.}}\)

c) Vì điểm \(C\) là trung điểm của đoạn thẳng \(AB\) nên \(BC = AC = \frac{{AB}}{2} = \frac{{12}}{2} = 6{\rm{\;(cm)}}{\rm{.}}\)

⦁ Vì điểm \(A\) thuộc tia \[Ox\] và tia \(C\) thuộc tia đối của tia \(Ox\) nên điểm \(O\) nằm giữa hai điểm \(A\) và \(C\)

Do đó \(AC = CO + OA\)

Suy ra \(CO = AC - OA = 6 - 4 = 2{\rm{\;(cm)}}{\rm{.}}\)

⦁ Ta có điểm \(M\) nằm giữa \(C\) và \(B\) nên \(BC = BM + CM\)

Suy ra \(CM = BC - BM = 6 - 4 = 2{\rm{\;(cm)}}{\rm{.}}\)

⦁ Vì điểm \(C\) nằm giữa hai điểm \(M,\,\,O\) và  \(MC = CO = 2{\rm{\;cm}}\) nên điểm \(C\) là trung điểm của đoạn thẳng \(OM.\)

2) a) Khi kim giờ và kim phút thay nhau chỉ số 12 và số 6 thì tạo thành một góc có số đo bằng \(180^\circ .\)

b) Từ số 12 đến số 6 có 6 khoảng, như vậy, cứ hai kim lần lượt chỉ hai số cạnh nhau trên đồng hồ thì có số đo bằng \(\frac{{180^\circ }}{6} = 30^\circ .\)

Vậy góc tạo bởi kim phút và kim giờ lúc 2 giờ có số đo là \(2 \cdot 30^\circ  = 60^\circ .\)

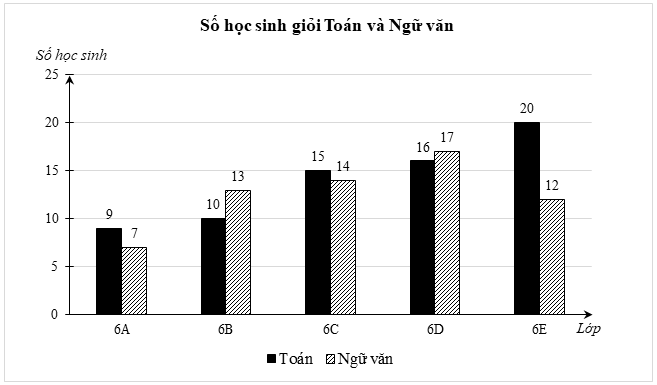
1) a) Số học sinh giỏi Toán của lớp 6E là nhiều nhất (20 bạn).

Số học sinh giỏi Ngữ văn của lớp 6A là ít nhất (7 bạn).

b) Số học sinh giỏi Toán của lớp 6C chiếm số phần trăm trong tổng số học sinh giỏi môn Toán của cả 5 lớp là: \(\frac{{15}}{{9 + 10 + 15 + 16 + 20}} \cdot 100\% \approx 21,43\% .\)

c) Bạn An nói lớp 6D có sĩ số là 34 học sinh có thể chưa đúng vì trong lớp có thể có học sinh không giỏi môn Toán, hoặc học sinh không giỏi môn Ngữ văn, hoặc học sinh giỏi cả hai môn.

2) Số chấm xuất hiện là số không vượt quá 4 là: 1 chấm, 2 chấm, 3 chấm, 4 chấm.

Số lần xuất hiện mặt có số chấm không vượt quá 4 là: \[15 + 20 + 18 + 22 = 75.\]

Xác suất thực nghiệm của sự kiện số chấm xuất hiện là số không vượt quá 4 là: \(\frac{{75}}{{100}} = \frac{3}{4}.\)