Bài 10: Số nguyên tố, Hợp số, Phân tích một số ra thừa số nguyên tố
19 người thi tuần này 4.6 7.5 K lượt thi 13 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 6 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 6 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 6 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 6 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 6 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 6 Chân trời sáng tạo có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 6 Chân trời sáng tạo có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 6 Chân trời sáng tạo có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
Lời giải:
Những số tự nhiên lớn hơn 1 và có ít ước nhất là 2; 3; 5; 7; 11; 13; …
Sau bài học này ta sẽ biết các số trên được gọi là số nguyên tố.
Lời giải
Lời giải:
a) Ư(1) = {1};
Ư(2) = {1; 2};
Ư(3) = {1; 3};
Ư(4) = {1; 2; 4};
Ư(5) = {1; 5};
Ư(6) = {1; 2; 3; 6};
Ư(7) = {1; 7};
Ư(8) = {1; 2; 4; 8};
Ư(9) = {1; 3; 9};
Ư(10) = {1; 2; 5; 10}.
b)
- Nhóm 1 chỉ có số 1.
- Nhóm 2 bao gồm 2; 3; 5; 7.
- Nhóm 3 bao gồm 4; 6; 8; 9; 10.
Lời giải
Lời giải:
a) Ta có: Ư(11) = {1; 11}; Ư(12) = {1; 2; 3; 4; 6; 12} và Ư(25) = {1; 5; 25}.
Số nguyên tố là 11 vì 11 lớn hơn 1 và chỉ có hai ước là 1 và chính nó.
Hợp số là: 12; 25 vì 12 có nhiều hơn 2 ước, còn 25 có 3 ước.
b) Không. Vì còn có số 0 và số 1 không phải là số nguyên tố và cũng không là hợp số.
Lời giải
Lời giải:
Phân tích số 60 ra thừa số nguyên tố theo cột dọc, ta được:
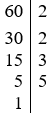
Vậy 60 = 2.2.3.5 = 22.31.51.
Lời giải
Lời giải:
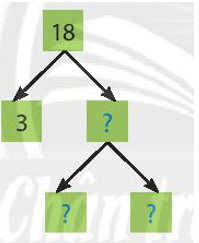
a)
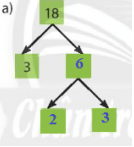
18 = 2.32.
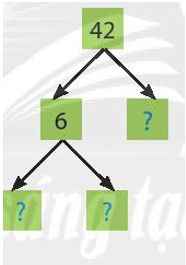
b)
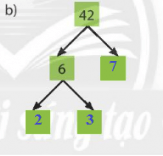
42 = 2.3.7
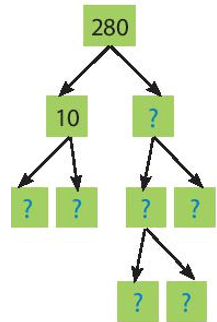
c)
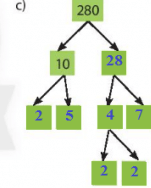
280 = 23.5.7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.