Câu hỏi:

12/07/2024 834

Cho $ΔABC$ , gọi D, E, F lần lượt là trung điểm của các cạnh AB, AC, BC; và M, N, P, Q theo thứ tự là trung điểm các đoạn thẳng DA, AE, EF, FD.

a) Chứng minh: EF là đường trung bình của tam giác ABC

b) Chứng minh: Các tứ giác DAEF; MNPQ là hình bình hành

c) Khi tam giác ABC vuông tại A thì các tứ giác DAEF; MNPQ là hình gì ? Chứng minh?
d) Tìm điều kiện của tam giác ABC để tứ giác MNPQ là hình vuông?

Xem lời giải

Câu hỏi trong đề: Bài tập theo tuần Toán 8 - Tuần 10 !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

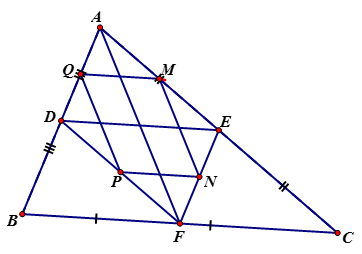
Cho ΔABC, gọi D, E, F lần lượt là trung điểm của các cạnh AB, AC, BC; và M, N, P, Q theo thứ tự là trung điểm các đoạn thẳng DA, AE, EF, FD. (ảnh 1)

a) Ta có E là trung điểm AC, F là trung điểm BC nên EF là đường trung bình $ΔABC$

b) Ta có EF là đường trung bình $ΔABC$ (cmt) $\Rightarrow EF / / AB & EF = \frac{1}{2} AB$ mà D là trung điểm AB nên $\Rightarrow \{\begin{cases} EF = AD \\ EF / / AD \end{cases}$ $\Rightarrow ADFE$ là hình bình hành

Xét $ΔADE$ có M, N lần lượt là trung điểm AD, AE $\Rightarrow MN / / DE & MN = \frac{1}{2} DE$

Cmtt

\Rightarrow PQ / / DE & PQ = \frac{1}{2} DE \Rightarrow PQ = MN & PQ / / MN \Rightarrow PQMN

là hình bình hành

c) Khi $ΔABC$ vuông tại A thì $\hat{A} = 90 ° \Rightarrow$ Hình bình hành DAEF có $\hat{A} = 90 °$ nên DAEF là hình chữ nhật.

Khi $\hat{A} = 90 °$ thì DAEF là hình chữ nhật $\Rightarrow AF = DE$

Mặt khác, theo tính chất đường trung bình ta có $MN = \frac{1}{2} DE, NP = \frac{1}{2} AF$ khi đó MN = NP

=> MNPQ là hình bình hành có MN = NP nên MNPQ là hình thoi

d) $ΔABC$ vuông tại A thì MNPQ là hình thoi. Để MNPQ là hình vuông thì $MN ⊥ NP$ mà

MN // DE, NP // AF (tính chất đường trung bình)

Nên $DE ⊥ AF$ mà DE // BC (tính chất đường trung bình) $\Rightarrow AF ⊥ BC$

Suy ra $ΔABC$ vuông tại A có AF là vừa đường trung tuyến, vừa đường cao

Nên $ΔABC$ vuông cân tại A

Vậy

ΔABC

vuông cân tại A thì MNPQ là hình vuông.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình bình hành ABCD Trên đường chéo BD lấy điểm E và K sao cho BE = DK

a) Chứng minh rằng AKCE là hình bình hành

b) Hình bình hành ABCD có điều kiện gì để AKCE là hình thoi

c) Gọi M là giao điểm của AK và CD. Xác định vi trí của điểm K để M là trung điểm của CD

Xem đáp án

Lời giải

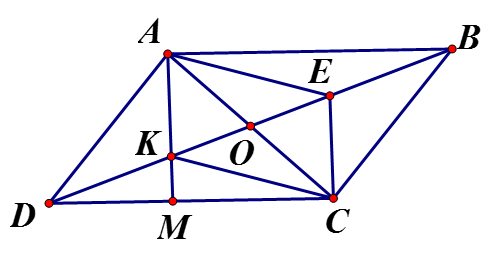
Cho hình bình hành ABCD Trên đường chéo BD lấy điểm E và K sao cho BE = DK (ảnh 1)

a) Gọi O là giao điểm của AC và BD. Vậy OA = OC, OB = OD mà BE = DK

\Rightarrow OK = OE \Rightarrow AKDE

là hình bình hành.

b) Để AKCE là hình thoi thì

AC ⊥ KE \Rightarrow AC ⊥ BD

Vậy ABCD là hình thoi thì AKCE là hình thoi

c) Để M là trung điểm DC thì K là trọng tâm

ΔABC

\Rightarrow DK = \frac{2}{3} DO

mà

DO = \frac{1}{2} DB \Rightarrow DK = \frac{1}{3} DB

Câu 2

Cho $ΔABC$ vuông tại A $(AB > AC),$ M là trung điểm của $AB, P$ là điểm nằm trong $ΔABC$ sao cho $MP ⊥ AB .$ Trên tia đối của tia MP lấy điểm Q sao cho MP = MQ

a) Chứng minh: tứ giác APBQ là hình thoi.

b) Qua C vẽ đường thẳng song song với BP cắt tia QP tại E. Chứng minh tứ giác ACEQ là hình bình hành.

c) Gọi N là giao điểm của PE và BC. Chứng minh: AC = 2MN

d) Cho $MN = 3 cm, AN = 5 cm .$ Tính chu vi $ΔABC$ .

Xem đáp án

Lời giải

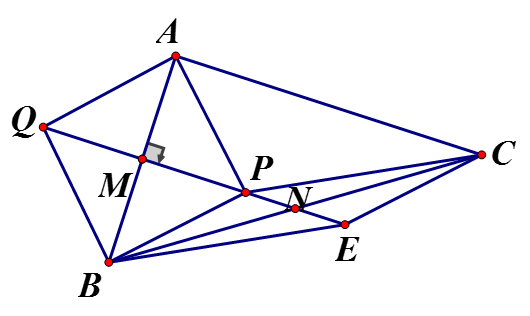
cho tam giác ABC vuông tại A (AB > AC) M là trung điểm của AB, P là điểm nằm trong tam giác ABC sao cho MP vuông AB (ảnh 1)

a) Tứ giác AQBP có $QP ⊥ AB, AM = MB, QM = MP \Rightarrow AQBP$ là hình thoi

b) Ta có: $AQ / / EC$ (cùng $/ / BP do AQBP$ là hình thoi) và $QE / / AC$ (cùng $⊥ AB)$

$\Rightarrow QACE$ là hình bình hành

c) Vì AQBP là hình thoi nên $MP = \frac{1}{2} PQ (1)$

Ta có: $BP / / EC (gt); BP = EC (= QA) \Rightarrow BPCE$ là hình bình hành nên PE cắt BC tại trung điểm N mỗi đường nên $NP = \frac{1}{2} PE (2)$

Cộng (1) và (2) vế theo vế ta có: $MP + NP = \frac{1}{2} (PQ + PE) \Rightarrow MN = \frac{1}{2} QE$

Mà QE = AC (tính chất hình bình hành) nên AC = 2MN

d) $AN = 5 cm \Rightarrow BC = 10 cm$ (Do N là trung điểm BC và AN là đường trung tuyến ứng với cạnh huyền)

$MN = 3 cm \Rightarrow AC = 6 cm \Rightarrow AB = \sqrt{{BC}^{2} - {AC}^{2}} = \sqrt{10^{2} - 6^{2}} = 8 cm ($ Áp dụng Pytago)

Nên chu vi $ΔABC : AB + AC + BC = 8 + 6 + 10 = 24 (cm)$

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu