Cho đường tròn và điểm M cách một khoảng bằng 20 cm. Kẻ tiếp tuyến MA ( là tiếp điểm) và kẻ dây vuông góc với OM. Chứng minh MB là tiếp tuyến của đường tròn (O).
Cho đường tròn và điểm M cách một khoảng bằng 20 cm. Kẻ tiếp tuyến MA ( là tiếp điểm) và kẻ dây vuông góc với OM. Chứng minh MB là tiếp tuyến của đường tròn (O).
Quảng cáo
Trả lời:
Phân tích đề bài
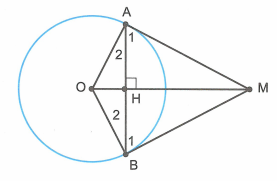
là tiếp tuyến của đường tròn (O)
Giải chi tiết
Gọi . Xét và có: OA = (bán kính đường tròn (O));
(giả thiết);
OH chung.
Suy ra (cạnh huyền – cạnh góc vuông) (hai cạnh tương ứng).
Tam giác MAB có MH vừa là đường cao đồng thời là đường trung tuyến nên cân tại M
(hai góc ở đáy).
Lại có cân tại O nên . Khi đó .
Suy ra . Vậy MB là tiếp tuyến của đường tròn (O).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phân tích đề bài
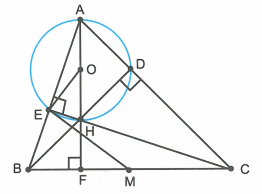
a) Thấy ngay hai tam giác AEH và ADH là hai tam giác vuông có chung cạnh huyền nên bốn điểm A, D, H, E cùng nằm trên đường tròn đường kính AH.
b) EM là tiếp tuyến của (O)
Giải chi tiết
a) Gọi O là trung điểm của AH.
Theo giả thiết và là các tam giác vuông có chung cạnh huyển AH nên bốn điểm A, D, H, E cùng nằm trên đường tròn (O) đường kính AH.
b) Xét tam giác OAE có OE = OA nên cân tại O . (1)
Tương tự cân tại M nên . (2)
Gọi .
Lại có: (vì cùng phụ với ). (3)
Từ (1), (2) và (3) suy ra .
Ta có: .
Vậy ME là tiếp tuyến của đường tròn (O).
Lời giải
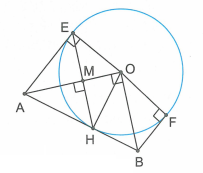
a) Theo giả thiết, tại M nên M là trung điểm của EH (quan hệ đường kính và dây cung).
.
Áp dụng định lí Pytago trong tam giác QEM có:
.
Vậy độ dài dây EH là 8 cm.
b) cân tại A vì có AM vừa là đường cao, đồng thời là đường trung tuyến.
.
Xét và có: OE = OH (bán kính đường tròn (O));
AE = AH (chứng minh trên);
OA chung.
(hai góc tương ứng).
Hay . Vậy AH là tiếp tuyến của đường tròn (O).
c) Ta thấy B là giao của hai tiếp tuyến BH và BF nên .
Lại có nên .
Tức là ba điểm E, O, F thẳng hàng.
Theo tính chất của hai tiếp tuyến cắt nhau ta có: FB = BH, EA =HA.
Áp dụng hệ thức lượng trong tam giác vuông OAB ta có: .
Vậy . (1)
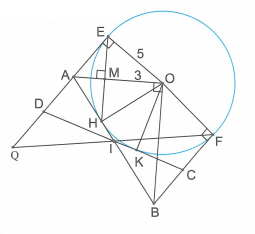
d) Ta có (vì cùng vuông góc với EF).
(*).
Dễ dàng chứng minh được vuông tại O.
Áp dụng hệ thức lượng trong tam giác vuông COD, với OK là đường cao, ta có: .
Mà DE, DK là các tiếp tuyến của (O) cắt nhau tại D nên DE = DK.
Tương tự, CK = CF.
(2)
Từ (1) và (2) suy ra: (**)
Từ (*) và (**) suy ra: .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.