Câu hỏi:

13/07/2024 64,973

Cho tam giác $A B C$ có hai đường cao BD và $C E$ cắt nhau tại $H$ .

a) Chứng minh rằng bốn điểm A, D, H , cùng nằm trên một đường tròn (gọi tâm của nó là O ).

b) Gọi M là trung điểm của $B C$ . Chứng minh rằng ME là tiếp tuyến của đường tròn (O).

Câu hỏi trong đề: Trắc nghiệm Chuyên đề Toán 9 Chuyên đề 3: Vị trí tương đối của đường thằng và đường tròn. Vị trí tương đối của hai đường tròn có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phân tích đề bài

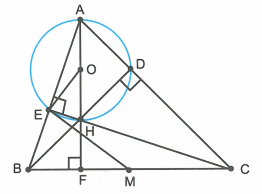
a) Thấy ngay hai tam giác AEH và ADH là hai tam giác vuông có chung cạnh huyền nên bốn điểm A, D, H, E cùng nằm trên đường tròn đường kính AH.

b) EM là tiếp tuyến của (O)

$⇕$

$\hat{O E M} = 90 °$

$⇕$

$\hat{A E O} = \hat{C E M}$

$⇕$

$\hat{E A O} = \hat{E C B}$

Giải chi tiết

a) Gọi O là trung điểm của AH.

Theo giả thiết $Δ A E H$ và $Δ A D H$ là các tam giác vuông có chung cạnh huyển AH nên bốn điểm A, D, H, E cùng nằm trên đường tròn (O) đường kính AH.

b) Xét tam giác OAE có OE = OA nên $Δ O A E$ cân tại O $\Rightarrow \hat{O A E} = \hat{O E A}$ . (1)

Tương tự $Δ M E C$ cân tại M nên $\hat{M E C} = \hat{M C E}$ . (2)

Gọi $F = A H \cap B C \Rightarrow A F ⊥ B C$ .

Lại có: $\hat{E C B} = \hat{B A F}$ (vì cùng phụ với $\hat{A B F}$ ). (3)

Từ (1), (2) và (3) suy ra $\hat{M E C} = \hat{A E O}$ .

Ta có: $\hat{O E M} = \hat{O E H} + \hat{H E M} = \hat{O E H} + \hat{A E O} = \hat{A E H} = 90 °$ .

Vậy ME là tiếp tuyến của đường tròn (O).

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho đường tròn (0; R) và điểm A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn (O) (với E là tiếp điểm). Vẽ dây EH vuông góc với AO tại M.

a) Cho biết bán kính R = 5cm, OM = 3cm. Tính độ dài dây EH.

b) Chứng minh AH là tiếp tuyến của đường tròn (O).

c) Đường thẳng qua O vuông góc với OA cắt AH tại B. Vẽ tiếp tuyến BF với đường tròn (O) (F là tiếp điểm). Chứng minh ba điểm E, O, F thẳng hàng và $B F . A E = R^{2}$ .

d) Trên tia HB lấy điểm $I (I \neq B)$ , qua I vẽ tiếp tuyến thứ hai với đường tròn (O) cắt các đường thẳng BF, AE lần lượt tại C và D. Vẽ đường thẳng IF cắt AE tại Q.

Chứng minh AE = DQ.

Xem đáp án

Lời giải

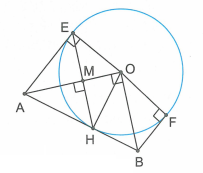
Media VietJack

a) Theo giả thiết, $E H ⊥ O A$ tại M nên M là trung điểm của EH (quan hệ đường kính và dây cung).

$\Rightarrow E H = 2 E M$ .

Áp dụng định lí Pytago trong tam giác QEM có:

$O M^{2} + E M^{2} = O E^{2} \Rightarrow E M = \sqrt{O E^{2} - O M^{2}} = \sqrt{5^{2} - 3^{2}} = 4 cm$

$\Rightarrow E H = 2 E M = 8 cm$ .

Vậy độ dài dây EH là 8 cm.

b) $Δ A E H$ cân tại A vì có AM vừa là đường cao, đồng thời là đường trung tuyến.

$\Rightarrow A E = A H$ .

Xét $Δ O E A$ và $Δ O H A$ có: OE = OH (bán kính đường tròn (O));

AE = AH (chứng minh trên);

OA chung.

$\Rightarrow Δ O E A = Δ O H A (c.c.c) \Rightarrow \hat{O H A} = \hat{O E A} = 90 °$ (hai góc tương ứng).

Hay $A H ⊥ O H$ . Vậy AH là tiếp tuyến của đường tròn (O).

c) Ta thấy B là giao của hai tiếp tuyến BH và BF nên $\hat{B O F} = \hat{B O H}$ .

Lại có $\hat{E O A} = \hat{H O A}$ nên $\hat{E O A} + \hat{A O B} + \hat{B O F} = 2 (\hat{A O H} + \hat{B O H}) = 180 °$ .

Tức là ba điểm E, O, F thẳng hàng.

Theo tính chất của hai tiếp tuyến cắt nhau ta có: FB = BH, EA =HA.

Áp dụng hệ thức lượng trong tam giác vuông OAB ta có: $B H . H A = O H^{2}$ .

Vậy $B F . A E = R^{2}$ . (1)

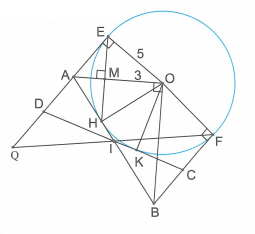
Media VietJack

d) Ta có $B F // A Q$ (vì cùng vuông góc với EF).

$\frac{B F}{A Q} = \frac{I F}{I Q} = \frac{C F}{Q D} \Rightarrow \frac{B F}{C F} = \frac{A Q}{D Q}$ (*).

Dễ dàng chứng minh được $Δ C O D$ vuông tại O.

Áp dụng hệ thức lượng trong tam giác vuông COD, với OK là đường cao, ta có: $O K^{2} = D K . C K$ .

Mà DE, DK là các tiếp tuyến của (O) cắt nhau tại D nên DE = DK.

Tương tự, CK = CF.

$\Rightarrow O K^{2} = C F . D E \Leftrightarrow C F . D E = R^{2}$ (2)

Từ (1) và (2) suy ra: $C F . D E = A E . B F \Leftrightarrow \frac{B F}{C F} = \frac{D E}{A E}$ (**)

Từ (*) và (**) suy ra:

\frac{A Q}{D Q} = \frac{D E}{A E} \Leftrightarrow \frac{A Q - D Q}{D Q} = \frac{D E - A E}{A E} \Leftrightarrow \frac{A D}{D Q} = \frac{A D}{A E} \Leftrightarrow A E = D Q

Câu 2

Cho đường tròn $(O; 12 cm)$ và điểm M cách một khoảng bằng 20 cm. Kẻ tiếp tuyến MA ( là tiếp điểm) và kẻ dây vuông góc với OM. Chứng minh MB là tiếp tuyến của đường tròn (O).

Xem đáp án

Lời giải

Phân tích đề bài

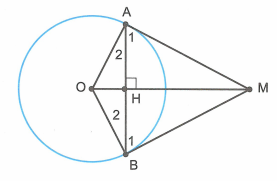
Media VietJack

là tiếp tuyến của đường tròn (O)

$⇕$

$O B ⊥ B M$

$⇕$

$\hat{O B M} = 90 °$

$⇕$

$\hat{O B M} = \hat{O A M}$

Giải chi tiết

Gọi $H = O M \cap A B$ . Xét $Δ O A H$ và $Δ O B H$ có: OA = (bán kính đường tròn (O));

$\hat{O H A} = \hat{O H B} = 90 °$ (giả thiết);

OH chung.

Suy ra $Δ O A H = Δ O B H$ (cạnh huyền – cạnh góc vuông) $\Rightarrow H A = H B$ (hai cạnh tương ứng).

Tam giác MAB có MH vừa là đường cao đồng thời là đường trung tuyến nên $Δ M A B$ cân tại M

$\Rightarrow \hat{A_{1}} = \hat{B_{1}}$ (hai góc ở đáy).

Lại có $Δ O A B$ cân tại O nên $\hat{A_{2}} = \hat{B_{2}}$ . Khi đó $\hat{M B O} = \hat{B_{1}} + \hat{B_{2}} = \hat{A_{1}} + \hat{A_{2}} = \hat{O A M} = 90 °$ .