Câu hỏi:

19/08/2025 369

Cho điểm A₁ cố định, đoạn C₁D₁thuộc đường thẳng d có độ dài không đổi chuyển động trên đường thẳng này. Tìm vị trí của $C_{1} D_{1}$ để chu vi tam giác $A_{1} C_{1} D_{1}$ bé nhất.

Xem lời giải

Câu hỏi trong đề: Trắc nghiệm Chuyên đề Toán 9 Chuyên đề 9: Bài toán thực tế Hình học có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

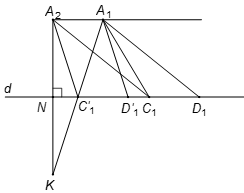
Cho điểm A1 cố định, đoạn C1D1 thuộc đường thẳng d có độ dài không đổi chuyển động trên (ảnh 1)

Để chứng minh chu vi của tam giác $A_{1} C_{1} D_{1}$ bé nhất, ta cần chứng minh $A_{1} C_{1} + A_{1} D_{1}$ bé nhất.

Dựng hình bình hành $A_{1} C_{1} D_{1} A_{2}$ (hình vẽ).

Gọi K là điểm đối xứng với A₂ qua đường thẳng d.
Nối $K A_{1}$ cắt đường thẳng d tại ${C^{'}}_{1}$ .

Dựng hình bình hành $A_{2} {C^{'}}_{1} {D^{'}}_{1} A_{1}$ .

Ta có

$C_{1} A_{1} + A_{1} D_{1} \geq C_{1} A_{1} + C_{1} A_{2} = C_{1} A_{1} + C_{1} K \geq A_{1} K = A_{1} {C^{'}}_{1} + {C^{'}}_{1} A_{2} = {C^{'}}_{1} A_{1} + {D^{'}}_{1} A_{1}$ .

Dấu “=” xảy ra khi C₁ trùng với ${C^{'}}_{1}$ .

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Hai điểm dân cư nằm về hai phía của một con sông rộng. Người ta muốn xây cầu qua sông (vuông góc với bờ sông) và làm đường nối hai khu dân cư qua chiếc cầu. Phải đặt vị trí cầu ở đâu, để quãng đường giữa hai điểm dân cư là nhỏ nhất (hình vẽ)?

Xem đáp án

Lời giải

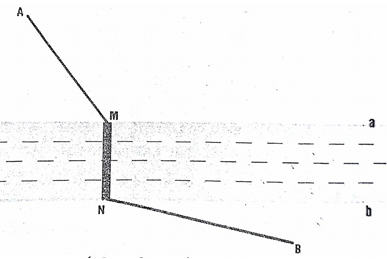
Giả sử nếu con sông rất đẹp, hẹp đến mức hai bờ sông a và b trùng nhau. Di chuyển điểm M, ta tìm được vị trí của M là giao điểm của bờ sông a và đoạn AB (Ta đã biết đây là bài toán quen thuộc: $M A + M B \geq A B \Rightarrow M A + M B$ ngắn nhất khi M là giao điểm của a và đoạn thẳng AB).

Từ đó ta cần tìm cách đưa ví dụ 1 về bài toán này. Ta làm như sau:

Dựng hình bình hành $A M N A^{'}$ : Ta có $A M = A^{'} N$ .

Vậy $A M + M N + N B = A A^{'} + A^{'} N + N B$ . Do AA' không đổi, nên $A^{'} N + N B$ nhỏ nhất khi N là giao điểm của A'B và bờ sông.

Cách dựng M, N:

- Dựng A' sao cho AMNA' là hình bình hành

- Dựng N là giao điểm của A'B và b.

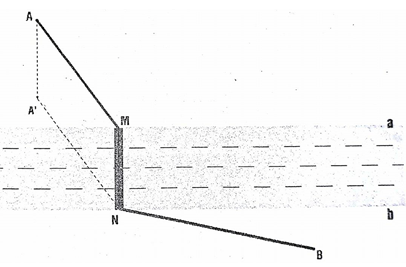
Hai điểm dân cư nằm về hai phía của một con sông rộng. Người ta muốn xây cầu qua sông (ảnh 2)

- Dựng M sao cho NM vuông góc với bờ sông a $(M \in a)$ .

- M, N là các vị trí cần tìm.

Câu 2

Cho hai điểm A, B cố định nằm cùng phía đối với đường thẳng d. Đoạn CD thuộc đường thẳng d có độ dài không đổi và chuyển động trên đoạn thẳng này. Tìm vị trí của CD để chu vi tứ giác ABCD nhỏ nhất.

Xem đáp án

Lời giải

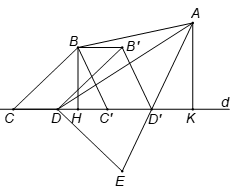
Cho hai điểm A, B cố định nằm cùng phía đối với đường thẳng d. Đoạn CD thuộc đường thẳng d (ảnh 1)

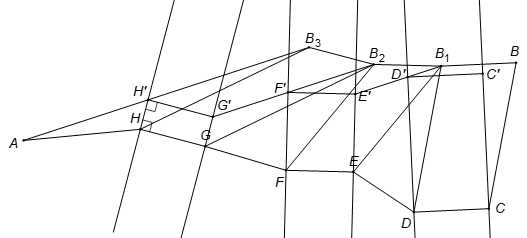
Dựng hình bình hành $B C D B^{'}$ .

Chu vi tứ giác ABCD nhỏ nhất khi BC+AD nhỏ nhất.

Hay $B^{'} D + A D$ nhỏ nhất.

Theo ví dụ 1, §, hệ thức này nhỏ nhất khi điểm D trùng với D' là giao của EA với d (E là điểm đối xứng của B' qua d).

Dựng hình bình hành $B B^{'} D^{'} C^{'}$ .

Ta có $B C + A D = B^{'} D + A D = D E + A D$

$\geq A E \Leftrightarrow B C + A D$

$\geq B^{'} D^{'} + A D^{'} = B C^{'} + A D^{'}$ .

Dấu “=” xảy ra khi CD trùng với C'D'.

Câu 3

Hai xóm A và B cách nhau hai nhánh sông. Tìm địa điểm bắc cầu CD trên nhánh sông đối diện hai với điểm A và địa điểm bắc cầu EG trên nhánh sông đối diện với điểm B sao cho tổng khoảng cách từ A đến C đến D đến E đến G rồi đến B là nhỏ nhất. Biết rằng góc tạo bởi hai nhánh sông là góc nhọn.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Hai điểm dân cư cách nhau ba con sông có lòng sông rộng khác nhau. Hãy bắc các cây cầu và làm đường nối hai điểm dân cư với con đường ngắn nhất (hình vẽ).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Cho điểm A₁ cố định, đoạn C₁D₁thuộc đường thẳng d có độ dài không đổi chuyển động trên đường thẳng này. Tìm vị trí của $C_{1} D_{1}$ để chu vi tam giác $A_{1} C_{1} D_{1}$ bé nhất.