Chủ đề 8: Dựng hình bình hành trong chứng minh các bài toán thực tiễn
21 người thi tuần này 4.6 13.9 K lượt thi 5 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
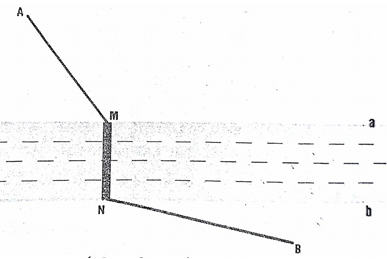
Giả sử nếu con sông rất đẹp, hẹp đến mức hai bờ sông a và b trùng nhau. Di chuyển điểm M, ta tìm được vị trí của M là giao điểm của bờ sông a và đoạn AB (Ta đã biết đây là bài toán quen thuộc: ngắn nhất khi M là giao điểm của a và đoạn thẳng AB).
Từ đó ta cần tìm cách đưa ví dụ 1 về bài toán này. Ta làm như sau:
Dựng hình bình hành : Ta có .
Vậy . Do AA' không đổi, nên nhỏ nhất khi N là giao điểm của A'B và bờ sông.
Cách dựng M, N:
- Dựng A' sao cho AMNA' là hình bình hành
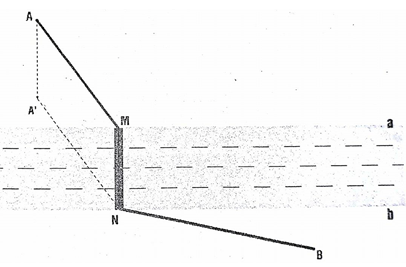
- Dựng M sao cho NM vuông góc với bờ sông a .
- M, N là các vị trí cần tìm.
Lời giải
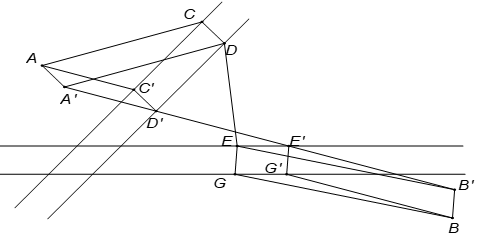
Dựng các hình bình hành .
Nối A', B' cắt các nhánh sông tại D' và E' như hình vẽ.
Từ D' và E' ta suy ra C' và G' bằng phép dựng vuông góc.
Ta sẽ chứng minh rằng C'D' và E'G' là các địa điểm cần dựng.
Thật vậy
.
Hay (đpcm).
Lời giải
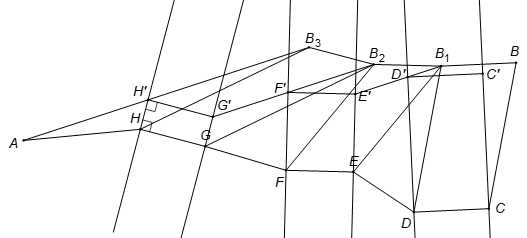
Gọi là ba cây cầu bất kì bắc qua ba con sông.
Dựng các hình bình hành .
Nối cắt bờ con sông thứ nhất đối diện với điểm A tại H'. Dựng vuông góc với bờ sông còn lại của con sông thứ nhất. Nối cắt bờ con sông thứ hai đối diện với G' tại F'. Dựng vuông góc với bờ sông còn lại của con sông thứ hai. Nối cắt bờ con sông thứ ba đối diện với điểm E' với D'. Dựng D'C' vuông góc với bờ sông còn lại của con sông thứ ba (hình vẽ). Ta có các cây cầu là các cây cầu cần dựng.
Thật vậy, .
Từ đây ta có điều phải chứng minh.
Lời giải
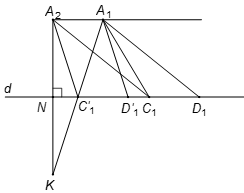
Để chứng minh chu vi của tam giác bé nhất, ta cần chứng minh bé nhất.
Dựng hình bình hành (hình vẽ).
Gọi K là điểm đối xứng với A2 qua đường thẳng d.
Nối cắt đường thẳng d tại .
Dựng hình bình hành .
Ta có
.
Dấu “=” xảy ra khi C1 trùng với .
Lời giải
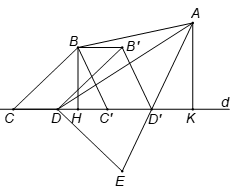
Dựng hình bình hành .
Chu vi tứ giác ABCD nhỏ nhất khi BC+AD nhỏ nhất.
Hay nhỏ nhất.
Theo ví dụ 1, §, hệ thức này nhỏ nhất khi điểm D trùng với D' là giao của EA với d (E là điểm đối xứng của B' qua d).
Dựng hình bình hành .
Ta có
.
Dấu “=” xảy ra khi CD trùng với C'D'.