Chủ đề 6: Phương pháp bất đẳng thức trong chứng minh các bài toán thực tế
21 người thi tuần này 4.6 13.9 K lượt thi 7 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
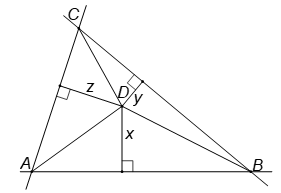
Giả sử các giao điểm của ba con đường là các đỉnh của một tam giác ABC và . Đặt khoảng cách từ điểm D bất kỳ đến các cạnh của tam giác lần lượt là x, y và z.
Khi đó diện tích của tam giác ABC bằng tổng diện tích của tam giác và ADC:
.
Từ đó ta có bất đẳng thức , trong đó dấu bất đắng thức chỉ xảy ra:
Hoặc khi z=y=0, nếu ,
Hoặc khi z=0, nếu ,
Hoặc khi z, y, z bất kỳ, nếu .
Như vậy, ứng với các trường hợp ta có kết luận:
- Xí nghiệp phải đặt ở đỉnh đối diện với cạnh lớn nhất.
- Nếu có hai cạnh lớn nhất bằng nhau, thì xí nghiệp đặt ở điểm bất kì trên cạnh nhỏ nhất.
- Nếu cả ba cạnh bằng nhau thì xí nghiệp đặt bất kì đầu trong tam giác kể cả trên một cạnh nào đó.
Lời giải
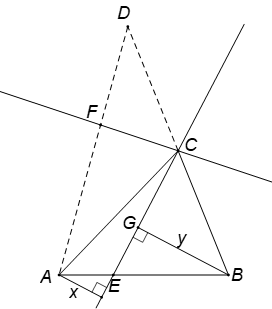
Giả sử (C là vị trí thành phố, còn B và A là vị trí của hai điểm dân cư). Gọi D là điểm đối xứng với B qua điểm C. Con đường ta cần tìm có thể cắt đoạn AB tại E hoặc cắt đoạn AD tại F.
1) Trường hợp thứ nhất.
Diện tích
Nghĩa là
2) Trường hợp thứ hai. Tương tự như phần 1 (x là khoảng cách từ A đến CF, y là khoảng cách từ B đến CF), diện tích
Nghĩa là: .
Vì vậy giá trị x+y nhỏ nhất khi các giá trị CE hoặc CF tương ứng càng lớn. Độ dài này lớn nhất khi .
Nếu hoặc trường hợp thì con đường đi qua B hoặc đi qua A đều như nhau.
Kết luận: Con đường phải đi qua điểm dân cư cách thành phố xa hơn, còn nếu thành phố C cách đều hai điểm dân cư thì con đường đi qua bất cứ điểm dân cư nào.
Lời giải
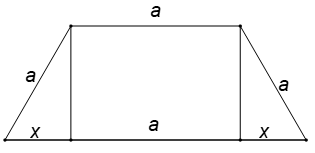
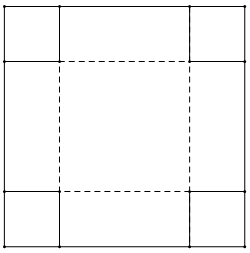
Đặt x là độ dài của hình chiếu cạnh bên hình thang xuống đáy lớn (bề rộng mương). Khi đó:
Hay:
Hoặc: .
Áp dụng hệ quả 3 ở trên ta có:
Vậy khi .
Lúc này, cạnh lớn của hình thang có chiều dài là 2a, góc nhọn của nó là 600.
Lời giải
Nếu ta ký hiệu y là thể tích của hình hộp chữ nhật, còn x là đương cao của hộp, thì: .
Ta có:
Dấu “=” xảy ra khi .
Kết luận: thể tích hình hộp lớn nhất là khi .
Lời giải
Ta kí hiệu x là độ dài của cạnh khu vườn mà nó vuông góc với con kênh. Khi đó độ dài của hàng rào được tính: .
Theo bất đẳng thức Cauchy, ta có: .
Như vậy P đạt được giá trị nhỏ nhất là khi , nghĩa là . Từ đây ta cũng tính được cạnh kia của hình chữ nhật.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.