khoahoc.vietjack.com
Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 9
  3. Toán

Câu hỏi:

19/08/2025 467 Lưu

Từ tất cả hình chữ nhật với chu vi đã cho, thì hình vuông có diện tích lớn nhất.

Xem lời giải

Câu hỏi trong đề: Trắc nghiệm Chuyên đề Toán 9 Chuyên đề 9: Bài toán thực tế Hình học có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

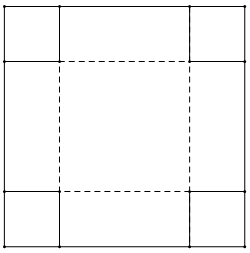
Đặt 2a là chu vi đã cho của những hình chữ nhật. Khi đó tổng x+y của hai cạnh hình chữ nhật x và y là một đại lượng không đổi a, nhưng diện tích xy là một biến số, mà ta muốn có giá trị lớn nhất.

Trung bình cộng của hai đại lượng là m=x+y2.

Ta kí hiệu d=x−y2, ta nhận được x=m+d,y=m−d.

Vì vậy: xy=(m+d)(m−d)=m2−d2=(x+y)24−d2.

Vì d2 là một số dương nên ta có: xy≤x+y2, ở đây dấu bằng thì xảy ra khi d=0 hoặc là x=y=m.

Đang tải chế độ Học...

Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay

Các sản phẩm khác của Vietjack:
  1. Combo 3 khóa học Toán - Văn - Anh lớp 1-12 chỉ với 250k
  2. Phòng luyện 1000 đề VIP Đgnl các trường ĐHQGHN, Tp.HCM, Bách Khoa, tốt nghiệp THPT chỉ với 399k
  3. Mã giảm giá 20% sản phẩm sách VietJack trên Shopee mall
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Từ một miếng bìa hình vuông cạnh a, người ta cắt bốn góc những hình vuông bằng nhau sao cho phần còn lại của miếng bìa theo những đường chấm thành một hộp có thể tích lớn nhất (hình vẽ).

Từ một miếng bìa hình vuông cạnh a, người ta cắt bốn góc những hình vuông bằng nhau sao (ảnh 1)

Lời giải

Nếu ta ký hiệu y là thể tích của hình hộp chữ nhật, còn x là đương cao của hộp, thì: y=(a−2x)2x.

Ta có: y=14(a−2x).(a−2x).4x

≤14a−2x+a−2x+4x33

=2a327

Dấu “=” xảy ra khi x=a6.

Kết luận: thể tích hình hộp lớn nhất là 2a327 khi x=a6.

Câu 2

Người ta đào một con mương với thiết diện cắt ngang là một hình thang cân, đáy và cạnh bên có cùng độ dài là a. Độ dài của đáy lớn (bề ngang của mặt mương) hình thang là bao nhiêu để diện tích của mặt cắt là lớn nhất (cho lưu lượng nước thoát qua lớn nhất).

Lời giải

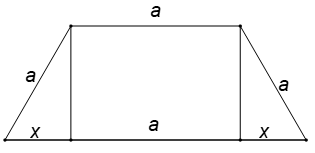
Người ta đào một con mương với thiết diện cắt ngang là một hình thang cân, đáy và cạnh bên (ảnh 1)
Người ta đào một con mương với thiết diện cắt ngang là một hình thang cân, đáy và cạnh bên có cùng

Đặt x là độ dài của hình chiếu cạnh bên hình thang xuống đáy lớn (bề rộng mương). Khi đó:

S=12(a+a+x+x).a2−x2=(a+x)a2−x2

Hay: S2=(a+x)3(a−x)

Hoặc: S2=13(a+x)(a+x)(a+x)(3a−3x),0<x<a.

Áp dụng hệ quả 3 ở trên ta có:

13(a+x)(a+x)(a+x)(3a−3x)

≤13a+x+a+x+a+x+3a−3x44

=133a24=2716a4

Vậy Smax=334a2 khi x=a2.

Lúc này, cạnh lớn của hình thang có chiều dài là 2a, góc nhọn của nó là 600.

Câu 3

Ba con đường cắt nhau tạo ra một tam giác. Trong tam giác đó phải đặt xí nghiệp ở đâu để tổng độ dài các con đường từ xí nghiệp ra các con đường là ngắn nhất?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong một đường tròn cho trước, hãy nội tiếp một hình chữ nhật có diện tích lớn nhất.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Bên cạnh một con sông đào thẳng người ta phải làm một khu vườn hình chữ nhật có diện tích cho trước S. Người ta muốn rào khu vườn bằng hàng rào ngắn nhất là bao nhiêu? Biết rằng về phía sông thì không phải làm hàng rào.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Hãy chọn hướng mở một con đường đi qua thành phố sao cho tổng các khoảng cách từ nó tới hai điểm dân cư đã có là nhỏ nhất.

Hãy chọn hướng mở một con đường đi qua thành phố sao cho tổng các khoảng cách từ nó tới (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bằng cách đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của VietJack.

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập