Cho ∆MNP cân tại M có \[\widehat {\rm{N}} = 50^\circ \] và MO là đường trung trực của NP (O ∈ NP). Số đo của \(\widehat {{\rm{OMP}}}\) là
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
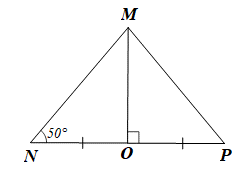
Do ∆MNP cân tại M nên \(\widehat {\rm{P}} = \widehat {\rm{N}} = 50^\circ \) (tính chất tam giác cân).
Vì MO là đường trung trực của NP nên MO ⊥ NP tại O.
Do đó ∆MOP vuông tại O.
Nên \(\widehat {{\rm{OMP}}} + \widehat {\rm{P}} = 90^\circ \)(tổng hai góc nhọn của tam giác vuông bằng 90°).
Hay \(\widehat {{\rm{OMP}}} + 50^\circ = 90^\circ \)
Suy ra \(\widehat {{\rm{OMP}}} = 90^\circ - 50^\circ = 40^\circ \).
Vậy ta chọn phương án A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
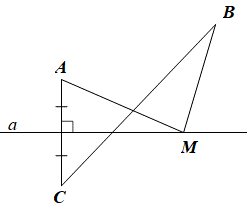
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: B

Vì OF là đường trung trực của ED (giả thiết)
Nên OE = OD và FE = FD (tính chất đường trung trực của đoạn thẳng).
Xét ∆OEF và ∆ODF có:
OE = OD (chứng minh trên),
FE = FD (chứng minh trên),
OF là cạnh chung.
Do đó ∆OEF = ∆ODF (c.c.c).
Suy ra \(\widehat {EOF} = \widehat {{\rm{DOF}}} = 30^\circ \)(hai góc tương ứng).
Mặt khác \(\widehat {{\rm{EOD}}} = \widehat {EOF} + \widehat {{\rm{FOD}}} = 30^\circ + 30^\circ = 60^\circ \).
Xét ∆OED có OE = OD nên ∆OED cân tại O.
Lại có \(\widehat {{\rm{EOD}}} = 60^\circ \)(chứng minh trên)
Do đó ∆OED đều.
Vậy ta chọn phương án B.
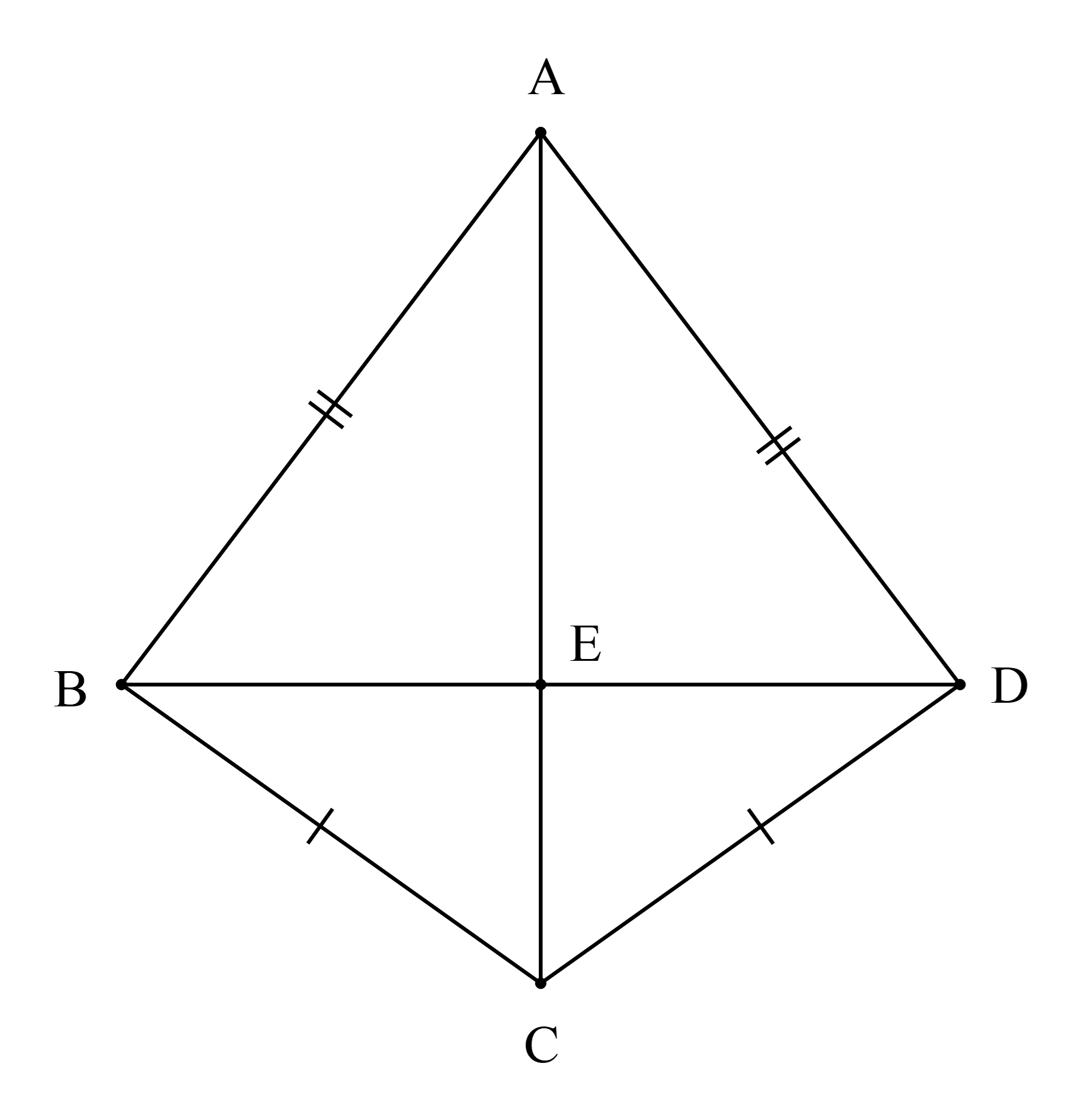
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
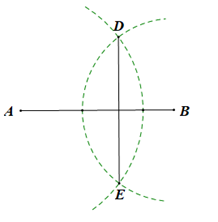
Ta có:
+) AD = AE (do D, E thuộc đường tròn tâm A)
Suy ra A nằm trên đường trung trực của DE.
+) BD = BE (do D, E thuộc đường tròn tâm B).
Suy ra B nằm trên đường trung trực của DE.
Do đó AB là đường trung trực của đoạn thẳng DE.
Vậy ta chọn đáp án D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.