Câu hỏi:
28/10/2022 2,015Cho tam giác DEF có DM, EN là hai đường trung tuyến cắt nhau tại G. Kéo dài DM lấy điểm H sao cho MH = MD. Kéo dài EN lấy điểm K sao cho NK = NE. Chọn khẳng định sai?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
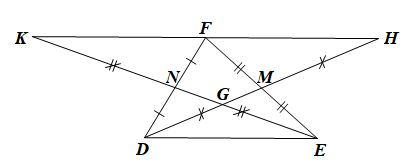
• Xét DKFN và DEDN có
NF = ND (vì N là trung điểm của DF),
\(\widehat {KNF} = \widehat {END}\) (hai góc đối đỉnh),
KN = EN (giả thiết)
Do đó DKFN = DEDN (c.g.c)
Suy ra KF = DE (hai cạnh tương ứng).
Do đó phương án A là đúng.
• Chứng minh tương tự ta cũng có: DFHM = DEDM (c.g.c)
Suy ra HF = DE (hai cạnh tương ứng).
Do đó phương án B là đúng.
• Do DFHM = DEDM (c.g.c) nên \(\widehat {MHF} = \widehat {MDE}\)(hai góc tương ứng)
Mà hai góc này ở vị trí so le trong
Suy ra FH // DE. Do đó phương án D là đúng.
Vậy ta chọn phương án C.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
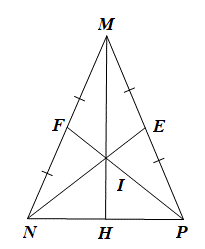
Xét DMNP có hai đường trung tuyến NE và PF cắt nhau tại I nên I là trọng tâm tam giác MNP.
Suy ra MH là đường trung tuyến của tam giác MNP.
Do đó H là trung điểm của NP hay NH = PH.
Vì tam giác MNP cân tại M nên MN = MP
Xét DMNH và DMPH có:
NH = PH (chứng minh trên),
MH là cạnh chung,
MN = MP (chứng minh trên)
Do đó DMNH = DMPH (c.c.c)
Suy ra \(\widehat {MHN} = \widehat {MHP}\) (hai góc tương ứng)
Mà \(\widehat {MHN} + \widehat {MHP} = 180^\circ \)(hai góc kề bù)
Do đó \(\widehat {MHN} = \widehat {MHP} = \frac{{180^\circ }}{2} = 90^\circ \)
Hay MH vuông góc NP tại trung điểm H của NP.
Suy ra MH là trung trực của NP.
Vậy ta chọn phương án C.
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
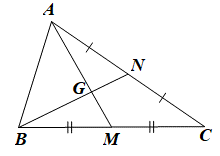
Gọi G là giao điểm của AM và BN.
Xét DABC có hai đường trung tuyến AM và BN cắt nhau tại G nên G là trọng tâm tam giác ABC.
Suy ra \({\rm{AG = }}\frac{2}{3}{\rm{AM}}\), \({\rm{BG = }}\frac{2}{3}{\rm{BN}}\)
Do đó \({\rm{MG = }}\frac{1}{3}{\rm{AM}}\), \({\rm{NG = }}\frac{1}{3}{\rm{BN}}\).
Mà AM = BN (giả thiết) nên AG = BG, MG = NG.
Xét ΔAGN và ΔBGM có
AG = BG (chứng minh trên),
\(\widehat {AGN} = \widehat {BGM}\) (hai góc đối đỉnh),
NG = MG (chứng minh trên)
Do đó ΔAGN = ΔBGM (c.g.c)
Suy ra AN = BM (hai cạnh tương ứng)
Lại có AN = \(\frac{1}{2}\)AC (vì N là trung điểm của AC);
BM = \(\frac{1}{2}\)BC (vì M là trung điểm của BC).
Nên AC = BC.
Suy ra tam giác ABC cân tại C.
Vậy ta chọn phương án B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2