Cho tam giác DEG có \(\widehat G = \widehat D + \widehat E\). Hai tia phân giác DA, EB cắt nhau tại H. Số đo góc AHB là:
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
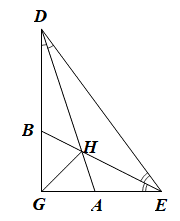
Vì DA là phân giác của góc GDE nên \(\widehat {GDA} = \widehat {E{\rm{D}}A} = \frac{1}{2}\widehat {G{\rm{D}}E}\).
Vì EB là phân giác của góc DEG nên \(\widehat {DEB} = \widehat {{\rm{GEB}}} = \frac{1}{2}\widehat {GED}\).
Do đó \(\widehat {E{\rm{D}}A} + \widehat {DEB} = \frac{1}{2}(\widehat {G{\rm{D}}E} + \widehat {{\rm{GED}}})\)
Xét DDGE có \(\widehat {GE{\rm{D}}} + \widehat {G{\rm{D}}E} + \widehat {EG{\rm{D}}} = 180^\circ \)(tổng ba góc trong một tam giác)
Mà \(\widehat {EG{\rm{D}}} = \widehat {GE{\rm{D}}} + \widehat {G{\rm{D}}E}\) (giả thiết)
Suy ra \(\widehat {EG{\rm{D}}} = \widehat {GE{\rm{D}}} + \widehat {G{\rm{D}}E} = 180^\circ :2 = 90^\circ \)
Do đó \(\widehat {E{\rm{D}}A} + \widehat {DEB} = \frac{1}{2}(\widehat {G{\rm{D}}E} + \widehat {{\rm{GED}}}) = \frac{1}{2}.90^\circ = 45^\circ \).
Xét DDHE có \(\widehat {DHE} + \widehat {DEH} + \widehat {H{\rm{D}}E} = 180^\circ \)(tổng ba góc trong một tam giác)
Suy ra \(\widehat {DHE} = 180^\circ - (\widehat {DEH} + \widehat {H{\rm{D}}E}) = 180^\circ - 45^\circ = 135^\circ \).
Lại có \(\widehat {AHB} = \widehat {DHE}\) (hai góc đối đỉnh)
Do đó \(\widehat {AHB} = 135^\circ \)
Vậy ta chọn phương án A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
C. 63°;
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
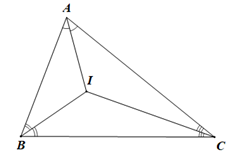
Trong DBIC có \(\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = {180^o}\) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {IBC} + \widehat {ICB} = 180^\circ - \widehat {BIC} = 180^\circ - 126^\circ = 54^\circ \).
Do BI là tia phân giác của góc ABC nên \(\widehat {IBC} = \frac{1}{2}\widehat {ABC}\);
Do CI là tia phân giác của góc ACB nên \(\widehat {ICB} = \frac{1}{2}\widehat {ACB}\).
Do đó \(\widehat {IBC} + \widehat {ICB} = \frac{1}{2}\widehat {ABC} + \frac{1}{2}\widehat {ACB} = \frac{1}{2}\left( {\widehat {ABC} + \widehat {ACB}} \right)\).
Suy ra \(\widehat {ABC} + \widehat {ACB} = 2.\left( {\widehat {IBC} + \widehat {ICB}} \right) = 2.54^\circ = 108^\circ \).
Trong DABC có \(\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {BAC} = 180^\circ - \left( {\widehat {ABC} + \widehat {ACB}} \right) = 180^\circ - 108^\circ = 72^\circ \).
Do AI là tia phân giác của góc BAC nên \(\widehat {BAI} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}.72^\circ = 36^\circ .\)
Vậy ta chọn phương án B.
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
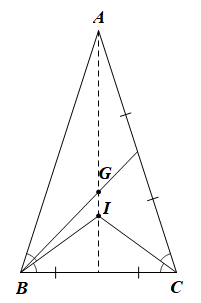
Vì I là giao điểm của các đường phân giác trong tam giác ABC nên I cách đều ba cạnh của ΔABC, do đó phương án A là sai.
Vì G là trọng tâm của tam giác ABC, không phải giao điểm ba đường trung trực nên G không cách đều ba đỉnh của ΔABC, do đó phương án C là sai.
Xét ΔABC cân tại A có AI là đường phân giác của góc BAC nên AI cũng là đường trung tuyến và AI đi qua trọng tâm G của tam giác ΔABC.
Suy ra A, I, G thẳng hàng nên phương án B là đúng.
Vậy ta chọn phương án B.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Cho tam giác AOM có \(\widehat A = 52^\circ \). Ba đường phân giác cắt nhau tại I. Số đo góc MIO là:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.