Cho tam giác ABC vuông tại A, tia phân giác góc B cắt AC tại D. Biết . Số đo góc ACB là
Cho tam giác ABC vuông tại A, tia phân giác góc B cắt AC tại D. Biết . Số đo góc ACB là
A. 150°;
B. 60°;
C. 30°;
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
Cho tam giác ABC vuông tại A nên
Vì BD là tia phân giác góc ABC nên
Ta có: (tổng 3 góc của một tam giác)
Thay số:
Suy ra:
Vậy .
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 55°;
B. 35°;
C. 90°;
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
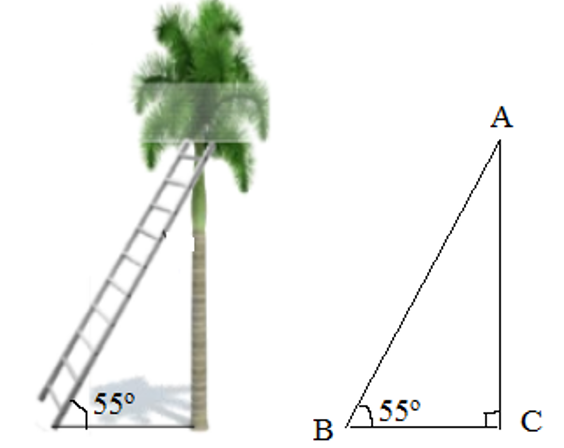
Ta vẽ tam giác ABC để mô tả hình ảnh chiếc thang dựa vào thân cây cau.
Tam giác ABC vuông tại C, ta có:
(tổng hai góc nhọn trong một tam giác)
Thay số:
Suy ra:
Vậy độ nghiêng của thang so với phương thẳng đứng là 35°.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Ta có: (tổng 3 góc của một tam giác)
Thay số:
Suy ra:
Nên
Vì FE // BD ⇒ (hai góc đồng vị)
Vậy .
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập