khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Vào học
Đăng nhập
Tạo VIP
Xin chào! Vào học
  2. Lớp 7
  3. Toán

Câu hỏi:

04/11/2022 2,197 Lưu

Cho tam giác ABC vuông tại A. Trên hai cạnh góc vuông AB và AC lấy lần lượt hai điểm M và N. So sánh MN và BC.

A. MN = BC;

B. MN < BC;

C. MN > BC;

D. Không đủ điều kiện để so sánh.
Xem lời giải

Câu hỏi trong đề: Trắc nghiệm Toán 7 Cánh diều Bài 2. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác (Phần 2) có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Hướng dẫn giải

Đáp án đúng là: B

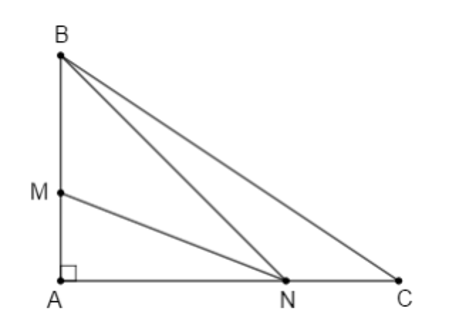
Cho tam giác ABC vuông tại A. Trên hai cạnh góc vuông AB và AC lấy lần lượt hai điểm (ảnh 1)

Tam giác MAN vuông tại A nên AMN^+ANM^=90° suy ra AMN^<90°

Ta có: AMN^+NMB^=180° (hai góc kề bù)

⇒NMB^=180°−AMN^>180°−90° 

⇒NMB^>90° hay góc NMB tù

Tam giác BMN có góc NMB tù nên BN là cạnh lớn nhất. Suy ra MN < BN (1)

Mặt khác, tam giác BAN vuông tại A nên BNA^+ABN^=90° suy ra BNA^<90°

Ta có: BNA^+BNC^=180° (hai góc kề bù)

⇒BNC^=180°−BNA^>180°−90° 

⇒BNC^>90° hay góc BNC tù

Tam giác BNC có góc BNC tù nên BC là cạnh lớn nhất. Suy ra BN < BC (2)

Từ (1) và (2) suy ra MN < BC.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Nhà An, Bình và Chi ở 3 địa điểm như hình vẽ. Ba bạn dự định học nhóm tại nhà của một trong ba bạn. Như vậy có hai bạn phải đi đến nhà của bạn còn lại. Để tổng quãng đường mà hai bạn đi là ngắn nhất thì nên họp nhóm tại nhà bạn nào?

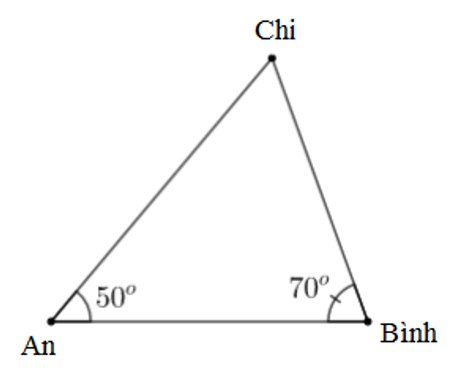
Nhà An, Bình và Chi ở 3 địa điểm như hình vẽ. Ba bạn dự định học nhóm tại nhà (ảnh 1)

A. nhà Chi;

B. nhà An;

C. nhà Bình;

D. Không đủ dữ kiện để xác định.

Lời giải

Hướng dẫn giải

Đáp án đúng là: C

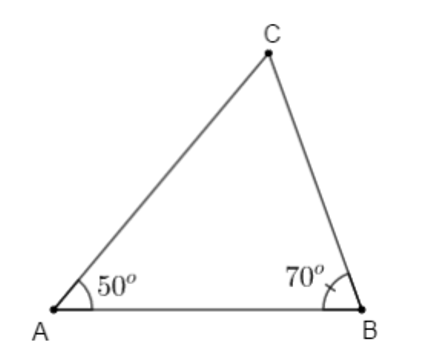
Nhà An, Bình và Chi ở 3 địa điểm như hình vẽ. Ba bạn dự định học nhóm tại nhà (ảnh 2)

Ta vẽ tam giác ABC để mô tả nhà ba bạn như hình vẽ.

Ta có: A^+B^+C^=180° (tổng ba góc của một tam giác)

Thay số: 50°+70°+C^=180°

Suy ra: 120°+C^=180°

Nên C^=60°

Suy ra: B^>C^>A^

Do đó: AC > AB > BC

Suy ra tổng AB + BC là nhỏ nhất.

Vậy để tổng quãng đường mà hai bạn đi là ngắn nhất thì nên họp nhóm tại nhà bạn Bình.

Câu 2

Cho tam giác ABC có B^+C^=A^ và 2B^=C^. Tia phân giác góc C cắt AB tại D. So sánh độ dài cạnh DB và DC đúng là

A. DB = DC;

B. DB > DC;

C. DB < DC;

D. Không đủ điều kiện để so sánh.

Lời giải

Hướng dẫn giải

Đáp án đúng là: A

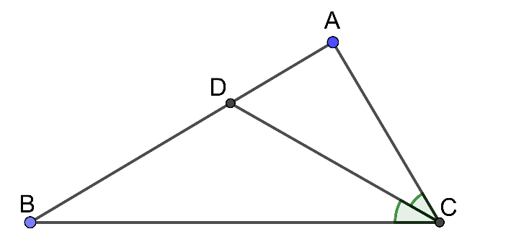
Cho tam giác ABC có góc B+ góc C= góc A và 2góc B= goc C. Tia phân giác góc C cắt AB tại D. (ảnh 1)

Ta có: A^+B^+C^=180° (tổng ba góc của một tam giác) mà B^+C^=A^ (giả thiết)

⇒B^+C^+B^+C^=180°

⇒2(B^+C^)=180°

⇒B^+C^=90°

Mặt khác 2B^=C^ (giả thiết) nên

B^+2B^=90°⇒3B^=90°⇒B^=90°:3⇒B^=30°

⇒C^=90°−30°=60°

Vì CD là phân giác của ACB^ nên DCB^=ACB^2=60°2=30°

Tam giác BDC có: B^=DCB^=30°

Do đó: DC = DB.

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack87. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập