Cho hai tam giác trong hình vẽ dưới đây.
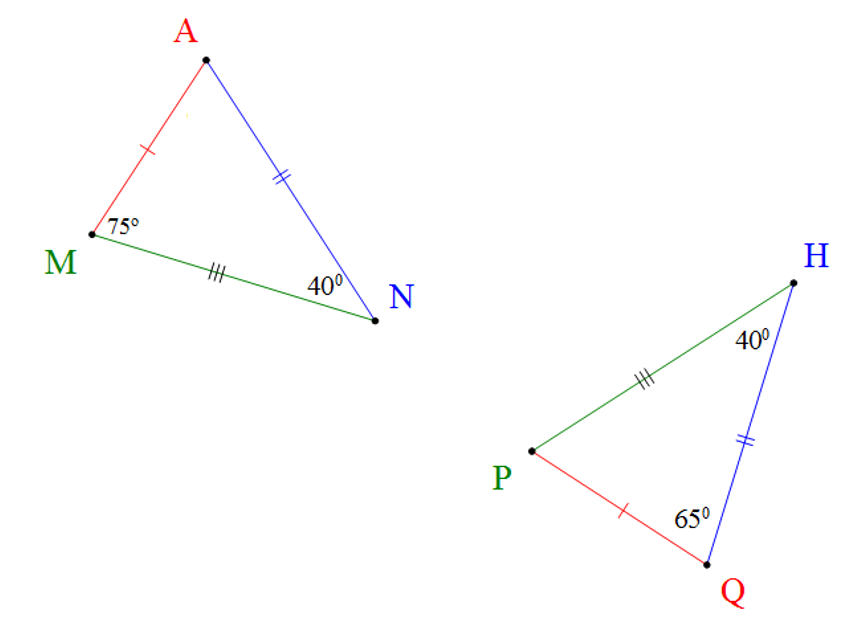
Khẳng định đúng là
Cho hai tam giác trong hình vẽ dưới đây.

Khẳng định đúng là
A. Hai tam giác không bằng nhau;
B. ∆AMN = ∆QHP;
C. ∆ANM = ∆QHP;
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
Tam giác AMN có: (tổng ba góc của một tam giác)
Suy ra:
Nên
Tam giác QHP có: (tổng ba góc của một tam giác)
Suy ra:
Nên
Suy ra: .
Mà AN = QH; AM = QP; NM = HP (hình vẽ)
Do đó ∆ANM = ∆QHP.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
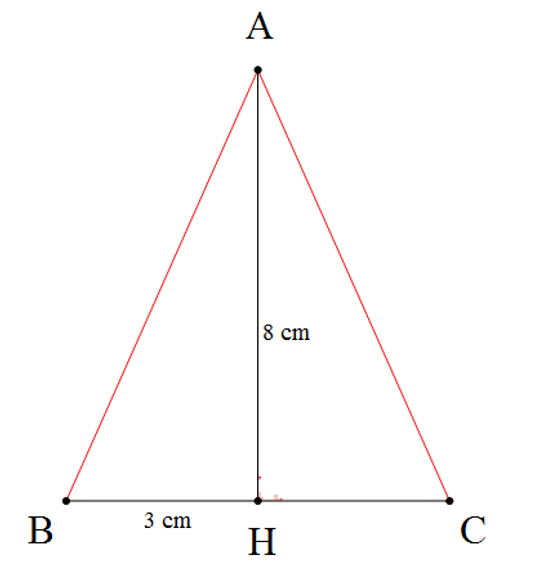
Câu 1
A. 12 cm2;
B. 24 cm2;
C. 6 cm2;
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Vì ∆ABH = ∆ACH (giả thiết)
Nên (các góc tương ứng bằng nhau)
Và HB = HC (các cạnh tương ứng bằng nhau). Suy ra HC = 3 cm.
Vì mà (hai góc kề bù)
Suy ra
Do đó AH ⊥ BC.
Nên diện tích tam giác AHC =Câu 2
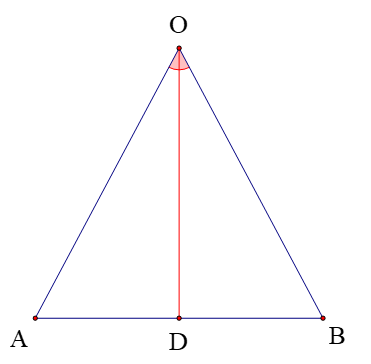
A. D là trung điểm của đoạn thẳng AB;
B. OD là tia phân giác của góc AOB;
C. OD ⊥ AB;
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Vì ∆OAD = ∆OBD (giả thiết)
Nên (các góc tương ứng bằng nhau)
Và OA = OB; AD = BD (các cạnh tương ứng bằng nhau)
Vì AD = BD và D thuộc AB nên D là trung điểm của đoạn thẳng AB.
Vì và tia OD nằm giữa 2 tia OA và OB nên OD là tia phân giác của góc AOB.
Vì mà (hai góc kề bù)
Suy ra
Do đó tam giác OAD và tam giác OBD là tam giác vuông. OD ⊥ AB.
Vậy D là khẳng định sai.