Cho khác góc bẹt, lấy điểm A thuộc tia Ox, điểm B thuộc tia Oy sao cho OA = OB. Lấy M là trung điểm của AB. Khẳng định nào dưới đây đúng?
Cho khác góc bẹt, lấy điểm A thuộc tia Ox, điểm B thuộc tia Oy sao cho OA = OB. Lấy M là trung điểm của AB. Khẳng định nào dưới đây đúng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
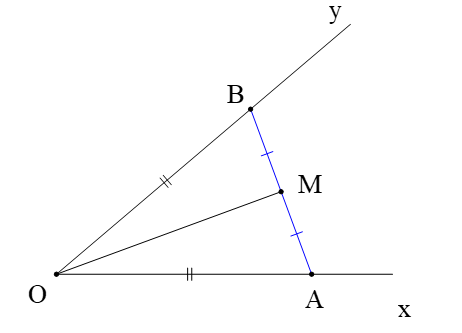
M là trung điểm của AB (giả thiết) nên MB = MA
Xét ∆OBM và ∆OMA có
OB = OA (giả thiết)
OM là cạnh chung
MB = MA (chứng minh trên)
Suy ra ∆OBM = ∆OAM (c.c.c)
Do đó (hai góc tương ứng)
(hai góc tương ứng)
Suy ra OM là tia phân giác góc BOA hay góc xOy.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
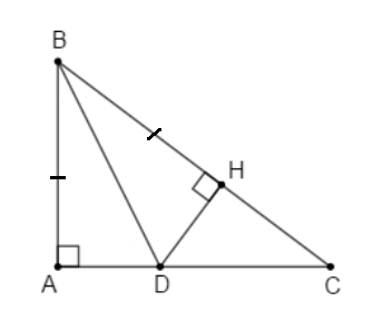
Xét hai tam giác vuông ABD và HBD có
AB = HB (giả thiết)
BD là cạnh chung
Suy ra ∆ABD = ∆HBD (cạnh huyền – cạnh góc vuông)
Do đó AD = HD (hai cạnh tương ứng)
Xét tam giác DHC vuông tại H nên:
DC > HD (mối quan hệ giữa cạnh và góc trong tam giác)
Do đó DC > AD hay AD < DC.
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
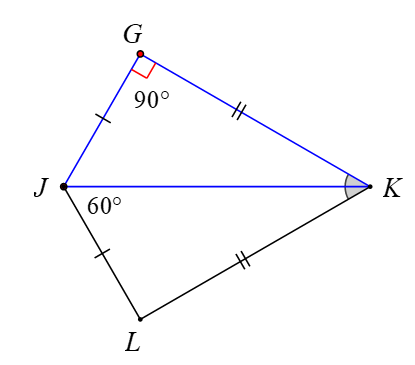
Xét hai tam giác JGK và JLK có:
JG = JL (theo giả thiết)
GK = LK (theo giả thiết)
JK là cạnh chung
Vậy (c.c.c)
⇒(hai góc tương ứng)
⇒
Xét tam giác JGK có: (tổng 3 góc của một tam giác)
⇒
Vì (chứng minh trên)
⇒ (hai góc tương ứng)
⇒
Vậy .
Nhắn tin Zalo