Câu hỏi:
31/01/2023 853
Có bao nhiêu giá trị nguyên dương của \[m\] để hàm số \[y = \sqrt {{{\left( {\sin x - \sqrt 3 \cos x} \right)}^2} - 2\sin x + 2\sqrt 3 \cos x - m + 3} \] xác định với mọi \[x \in \mathbb{R}\]?
Câu hỏi trong đề: Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án C
Phương pháp:
+ Đặt \[t = \sin x - \sqrt 3 \cos x\], tìm khoảng giá trị của \[t\].
+ Đưa hàm số về ẩn \[t\] trên miền giá trị đã xác định được, lập BBT và kết luận.
Cách giải:
\[y = \sqrt {{{\left( {\sin x - \sqrt 3 \cos x} \right)}^2} - 2\sin x + 2\sqrt 3 \cos x - m + 3} \]
\[y = \sqrt {{{\left( {\sin x - \sqrt 3 \cos x} \right)}^2} - 2\left( {\sin x - \sqrt 3 \cos x} \right) - m + 3} \]
+ Đặt \[t = \sin x - \sqrt 3 \cos x = 2\left( {\frac{1}{2}\sin x - \frac{{\sqrt 3 }}{2}\cos x} \right) = 2\sin \left( {x - \frac{\pi }{3}} \right) \Rightarrow - 2 \le t \le 2\]
Khi đó hàm số trở thành \[y = \sqrt {{t^2} - 2t - m + 3} \,\,\forall t \in \left[ { - 2;2} \right]\,\,\left( * \right)\].
+ Để hàm số ban đầu xác định với mọi \[x \in \mathbb{R}\] thì hàm số xác định với mọi \[t \in \left[ { - 2;2} \right]\].
Tức là \[{t^2} - 2t - m + 3 \ge 0\,\,\forall t \in \left[ { - 2;2} \right]\].
+ Xét hàm số \[f\left( t \right) = {t^2} - 2t - m + 3\] trên \[\left[ { - 2;2} \right]\] ta có BBT:
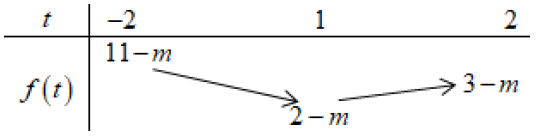
Để \[{t^2} - 2t - m + 3 \ge 0\,\,\forall t \in \left[ { - 2;2} \right]\] thì \[2 - m \ge 0 \Leftrightarrow m \le 2\].
Mà \[m\] nguyên dương \[ \Rightarrow m \in \left\{ {1;2} \right\}\].
Chú ý: Cần xác định chính xác khoảng giá trị của \[t\].
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án B
Phương pháp:
Công thức số hạng tổng quát của \[\left( {{u_n}} \right)\] có số hạng đầu \[{u_1}\] và công sai \[d\] là \[{u_n} = {u_1} + \left( {n - 1} \right)d\]
Cách giải:
Công thức số hạng tổng quát của \[\left( {{u_n}} \right)\] có số hạng đầu \[{u_1} = 3\] và công sai \[d = 2\] là
\[{u_n} = 3 + \left( {n - 1} \right)2 = 3 + 2n - 2 = 2n + 1\]
Lời giải
2) Một hộp có 6 bi đỏ, 7 bi xanh, 8 bi vàng (các bi khác nhau). Lấy ngẫu nhiên 6 bi. Tính xác suất để lấy được ít nhất 3 bi đỏ.
Phương pháp:
Sử dụng biến cố đối.
Cách giải:
Lấy ngẫu nhiên 6 viên bi \[ \Rightarrow n\left( \Omega \right) = C_{21}^6 = 54264\].
Gọi A là biến cố: “Lấy được ít nhất 3 viên bi đỏ” \[ \Rightarrow \overline A \]: “Lấy được ít hơn 3 viên bi đỏ”.
TH1: 0 bi đỏ + 6 bi khác màu đỏ (xanh hoặc vàng).
Số cách chọn là: \[C_6^0.C_{15}^6 = 5005\] cách.
TH2: 1 bi đỏ + 5 bi khác màu đỏ (xanh hoặc vàng).
Số cách chọn là: \[C_6^1.C_{15}^5 = 18018\] cách.
TH3: 2 bi đỏ + 4 bi khác màu đỏ (xanh hoặc vàng).
Số cách chọn là: \[C_6^2.C_{15}^4 = 20475\] cách.
Áp dụng quy tắc cộng ta có \[n\left( {\overline A } \right) = 5005 + 18018 + 20475 = 43498\].
Vậy \[P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{43498}}{{54264}} = \frac{{769}}{{3876}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
-
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
33 câu trắc nghiệm Toán 11 Kết nối tri thức Bài 29: Công thức cộng xác suất có đáp án
-
10 Bài tập Biểu diễn góc lượng giác trên đường tròn lượng giác (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận