Câu hỏi:
13/07/2024 2,638
Cho hình đa giác đều \[\left( H \right)\] có 36 đỉnh, chọn ngẫu nhiên 4 đỉnh của hình \[\left( H \right)\]. Tính xác suất để 4 đỉnh được chọn tạo thành hình vuông?
Câu hỏi trong đề: Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp:
+ Tính số phần tử của không gian mẫu.
+ Tính số phần tử của biến cố.
+ Tính xác suất của biến cố.
Cách giải:
Chọn ngẫu nhiên 4 đỉnh của hình \[\left( H \right) \Rightarrow n\left( \Omega \right) = C_{36}^4 = 58905\].
Giả sử \[{A_1},{A_2},{A_3},...,{A_{36}}\] là 36 đỉnh của đa giác đều \[\left( H \right)\]. Gọi \[O\] là tâm của đa giác đều \[\left( H \right)\].
\[ \Rightarrow {A_1}{A_2}...{A_{36}}\] là đa giác đều ngoại tiếp đường tròn \[\left( O \right)\].
Khi đó ta có \[{A_i}O{A_{i + 1}} = \frac{{360^\circ }}{{36}} = 10^\circ \,\,\forall i = \overline {1;36} \].
Để \[{A_x}{A_y}{A_z}{A_t}\] là hình vuông thì \[{A_x}O{A_y} = {A_y}O{A_z} = {A_z}O{A_t} = {A_t}O{A_x} = 90^\circ \].
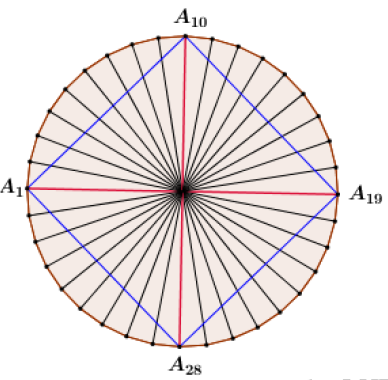
Ta có \[{O_1}O{A_{10}} = {A_{10}}O{A_{19}} = {A_{19}}O{A_{28}} = {A_{28}}O{A_1} = 90^\circ \Rightarrow {A_1}{A_{10}}{A_{19}}{A_{28}}\] là 1 hình vuông.
Cứ như vậy ta có các hình vuông là \[{A_2}{A_{11}}{A_{20}}{A_{29}},\,\,{A_3}{A_{12}}{A_{21}}{A_{30}},...,{A_9}{A_{18}}{A_{27}}{A_{36}}\].
Gọi A là biến cố: “4 đỉnh được chọn tạo thành hình vuông” \[ \Rightarrow n\left( A \right) = 9\].
Vậy \[P\left( A \right) = \frac{9}{{58905}} = \frac{1}{{6564}}\].
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025
Đã bán 244
₫ 136.000
₫ 58.000
Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025
Đã bán 104
₫ 136.000
₫ 38.000
Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack
Đã bán 1k
₫ 104.000
₫ 52.000
Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack
Đã bán 218
₫ 130.000
₫ 75.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cấp số cộng \[\left( {{u_n}} \right)\] có số hạng đầu \[{u_1} = 3\] và công sai \[d = 2\]. Công thức số hạng tổng quát của \[\left( {{u_n}} \right)\] là:
Xem đáp án »
31/01/2023
7,056
Câu 2:
2) Một hộp có 6 bi đỏ, 7 bi xanh, 8 bi vàng (các bi khác nhau). Lấy ngẫu nhiên 6 bi. Tính xác suất để lấy được ít nhất 3 bi đỏ.
2) Một hộp có 6 bi đỏ, 7 bi xanh, 8 bi vàng (các bi khác nhau). Lấy ngẫu nhiên 6 bi. Tính xác suất để lấy được ít nhất 3 bi đỏ.
Xem đáp án »
13/07/2024
6,276
Câu 4:
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành. Gọi \[O\] là giao điểm của \[AC\] và \[BD\]. \[M\] và \[N\] lần lượt là trung điểm của \[CD\] và \[SA\]. \[G\] là trọng tâm tam giác \[SAB\].
1) Tìm giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right)\].
2) Chứng minh \[MN\] song song với mặt phẳng \[\left( {SBC} \right)\].
3) Gọi \[\Delta \] là giao tuyến của hai mặt phẳng \[\left( {SAD} \right)\] và \[\left( {SMG} \right)\], \[P\] là giao điểm của đường thẳng \[OG\] và \[\Delta \]. Chứng minh \[P,N,D\] thẳng hàng.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành. Gọi \[O\] là giao điểm của \[AC\] và \[BD\]. \[M\] và \[N\] lần lượt là trung điểm của \[CD\] và \[SA\]. \[G\] là trọng tâm tam giác \[SAB\].
1) Tìm giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right)\].
2) Chứng minh \[MN\] song song với mặt phẳng \[\left( {SBC} \right)\].
3) Gọi \[\Delta \] là giao tuyến của hai mặt phẳng \[\left( {SAD} \right)\] và \[\left( {SMG} \right)\], \[P\] là giao điểm của đường thẳng \[OG\] và \[\Delta \]. Chứng minh \[P,N,D\] thẳng hàng.
Xem đáp án »
12/07/2024
5,501
Câu 6:
2) Tìm giá trị lớn nhất của hàm số \[y = 2\sqrt {\sin x + 1} - 3\].
2) Tìm giá trị lớn nhất của hàm số \[y = 2\sqrt {\sin x + 1} - 3\].
Xem đáp án »
13/07/2024
2,801
Câu 7:
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành tâm \[O\]. Giao tuyến của 2 mặt phẳng \[\left( {SAD} \right)\] và \[\left( {SBC} \right)\] là:
Xem đáp án »
31/01/2023
2,694
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
10 Bài tập Biến cố hợp. Biến cố giao (có lời giải)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
15 câu Trắc nghiệm Khoảng cách có đáp án (Nhận biết)
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
10 Bài tập Bài toán thực tiễn liên quan đến thể tích (có lời giải)
-
23 câu Trắc nghiệm Xác suất của biến cố có đáp án (Phần 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận