Câu hỏi:
01/02/2023 443
Tính tổng T các nghiệm của phương trình \[{\cos ^2}x = \sin x\cos x + 2\sin x - \cos x - 2\]trên khoảng\[\left( {\frac{\pi }{2};5\pi } \right).\]
Câu hỏi trong đề: Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án C
Phương pháp:
- Đưa phương trình về dạng tích.
- Giải các phương trình lượng giác cơ bản.
- Tìm nghiệm thuộc khoảng cho trước.
Cách giải:
\[{\cos ^2}x = \sin x\cos x + 2\sin x - \cos x - 2\]
\[ \Leftrightarrow 1 - {\sin ^2}x = \sin x\left( {\cos x + 2} \right) - \left( {\cos x + 2} \right)\]
\[ \Leftrightarrow \left( {1 - \sin x} \right)\left( {1 + \sin x} \right) = \left( {\cos x + 2} \right)\left( {\sin x - 1} \right)\]
\[ \Leftrightarrow \left( {\sin x - 1} \right)\left( {\cos x + 2 + 1 + \sin x} \right) = 0\]
\[ \Leftrightarrow \left( {\sin x - 1} \right)\left( {\sin x + \cos x + 3} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}\sin x = 1\\\sin x + \cos x = - 3\left( {\,Vo\,nghiem\,do\,{1^2} + {1^2} < {{\left( { - 3} \right)}^2}} \right)\end{array} \right.\]
\[ \Leftrightarrow x = \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\]
Xét\[x \in \left( {\frac{\pi }{2};5\pi } \right)\]ta có \[\frac{\pi }{2} < \frac{\pi }{2} + k2\pi < 5\pi \Leftrightarrow \frac{1}{2} < \frac{1}{2} + 2k < 5 \Leftrightarrow 0 < k < \frac{9}{4}.\]
Mà\[k \in \mathbb{Z} \Rightarrow k \in \left\{ {1;2} \right\} \Rightarrow x \in \left\{ {\frac{{5\pi }}{2};\frac{{9\pi }}{2}} \right\}.\]
Vậy \[T = \frac{{5\pi }}{2} + \frac{{9\pi }}{2} = 7\pi .\]
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án A
Phương pháp:
Xét trên đường tròn lượng giác.
Cách giải:
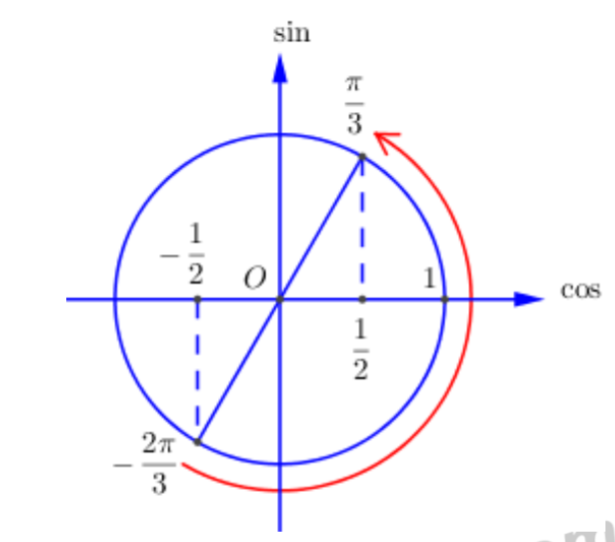
Ta có\[x \in \left[ { - \frac{\pi }{3};\frac{\pi }{6}} \right] \Rightarrow 2x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right].\]
Biểu diễn trên đường tròn lượng giác:
Dựa vào đường tròn lượng giác ta thấy với\[2x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right] \Rightarrow \cos 2x \in \left[ { - \frac{1}{2};1} \right].\]
Vậy\[M = 1;m = - \frac{1}{2} \Rightarrow T = M - 2m = 1 - 2.\left( { - \frac{1}{2}} \right) = 2.\]
Chú ý: Cần biểu diễn trên đường tròn lượng giác, nhiều học sinh nhầm lẫn\[2x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right] \Rightarrow \cos 2x \in \left[ { - \frac{1}{2};\frac{1}{2}} \right].\]
Lời giải
Phương pháp:
Liệt kê các bộ ba số có tổng bằng 11.
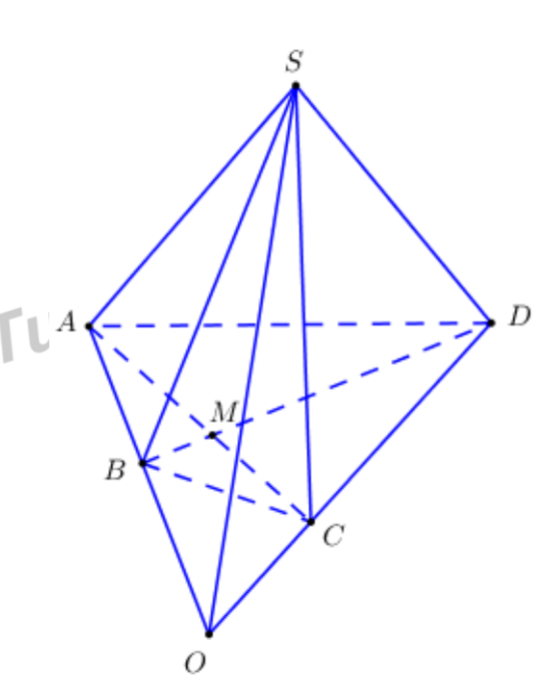
Cách giải:
Lấy ngẫu nhiên 3 thẻ từ một hộp 8 thẻ \[ \Rightarrow n\left( \Omega \right) = C_8^3 = 56\]cách.
Gọi A là biến cố: “Tổng các số ghi trên ba thẻ đó bằng 11”.
\[ \Rightarrow A = \left\{ {\left( {1;2;8} \right),\left( {1;3;7} \right),\left( {1;4;6} \right),\left( {2;3;6} \right),\left( {2;4;5} \right)} \right\} \Rightarrow n\left( A \right) = 5.\]
Vậy\[P\left( A \right) = \frac{5}{{56}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
Bài tập Tổ hợp - Xác suất cơ bản, nâng cao có lời giải chi tiết (P6)
-
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
-
15 câu Trắc nghiệm Khoảng cách có đáp án (Nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận