1. Lớp 11
  2. Toán
  3. Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án

Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 9)

33 người thi tuần này 4.6 12.8 K lượt thi 30 câu hỏi 90 phút

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

🔥 Học sinh cũng đã học

102 người thi tuần này

Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 10

2 K lượt thi 38 câu hỏi
42 người thi tuần này

Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 8

2 K lượt thi 38 câu hỏi
40 người thi tuần này

Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 7

2 K lượt thi 38 câu hỏi
33 người thi tuần này

Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 6

1.9 K lượt thi 38 câu hỏi
34 người thi tuần này

Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 5

1.9 K lượt thi 38 câu hỏi
64 người thi tuần này

Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 4

2 K lượt thi 38 câu hỏi
34 người thi tuần này

Bộ 10 đề thi cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 2

1.9 K lượt thi 39 câu hỏi
61 người thi tuần này

Bộ 10 đề thi cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 1

2 K lượt thi 39 câu hỏi

Danh sách câu hỏi:

Câu 1

Một người vào cửa hàng ăn, người đó chọn thực đơn gồm 1 món ăn trong 5 món khác nhau, 1 loại quả tráng miệng trong 5 loại quả tráng miệng khác nhau và một loại đồ uống trong 3 loại đồ uống khác nhau. Có bao nhiêu cách chọn thực đơn?
A. 13
B. 100
C. 75
D. 25

Lời giải

Đáp án C

Phương pháp:

Áp dụng quy tắc nhân.

Cách giải:

Số cách chọn 1 món ăn: 5 cách.

Số cách chọn 1 loại quả: 5 cách.

Số cách chọn 1 loại đồ uống: 3 cách.

Áp dụng quy tắc nhân ta có số cách chọn thực đơn là 5.5.3 = 75 cách.

Câu 2

Có bao nhiêu số nguyên m để phương trình \(12\sin x - 5\cos x = m\)có nghiệm.
A. 13
B. Vô số
C. 26
D. 27

Lời giải

Đáp án D

Phương pháp:

Phương trình \[a\sin x + b\cos x = c\]có nghiệm \[ \Leftrightarrow {a^2} + {b^2} \ge {c^2}.\]

Cách giải:

Phương trình \[12\sin x - 5\cos x = m\]có nghiệm \[ \Leftrightarrow {12^2} + {5^2} \ge {m^2} \Leftrightarrow {m^2} \le 169 \Leftrightarrow - 13 \le m \le 13.\]

Vậy có 27 số nguyên m thỏa mãn yêu cầu bài toán

Câu 3

Cho hình chóp S.ABCD, biết AC cắt BD tại M, AB cắt CD tại O. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD) .
A. SO
B. SM
C. SA
D. SC

Lời giải

Đáp án A

Phương pháp:

Xác định các điểm chung của hai mặt phẳng.

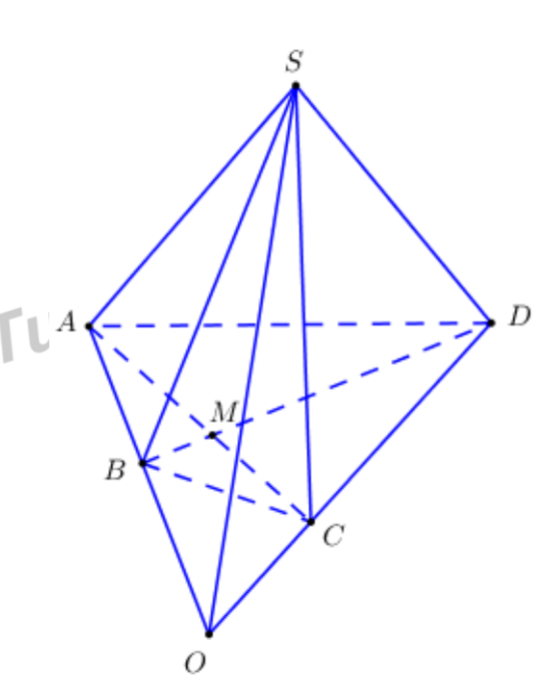
Media VietJack

Cách giải:

Ta có\[AB \cap CD = O \Rightarrow \left\{ \begin{array}{l}O \in AB \subset \left( {SAB} \right) \Rightarrow O \in \left( {SAB} \right)\\O \in CD \subset \left( {SCD} \right) \Rightarrow O \in \left( {SCD} \right)\end{array} \right..\]

\[ \Rightarrow O \in \left( {SAB} \right) \cap \left( {SCD} \right)\]

Lại có \[S \in \left( {SAB} \right) \cap \left( {SCD} \right).\]

Vậy \[\left( {SAB} \right) \cap \left( {SCD} \right) = SO.\]

Câu 4

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số\(y = \cos 2x\)trên đoạn\(\left[ { - \frac{\pi }{3};\frac{\pi }{6}} \right].\)Tính giá trị biểu thức\(T = M - 2m.\)
A. T = 2
B. \(T = 1 + \sqrt 3 \)
C. \(T = \frac{3}{2}\)
D. \(T = \frac{5}{2}\)

Lời giải

Đáp án A

Phương pháp:

Xét trên đường tròn lượng giác.

Media VietJack

Cách giải:

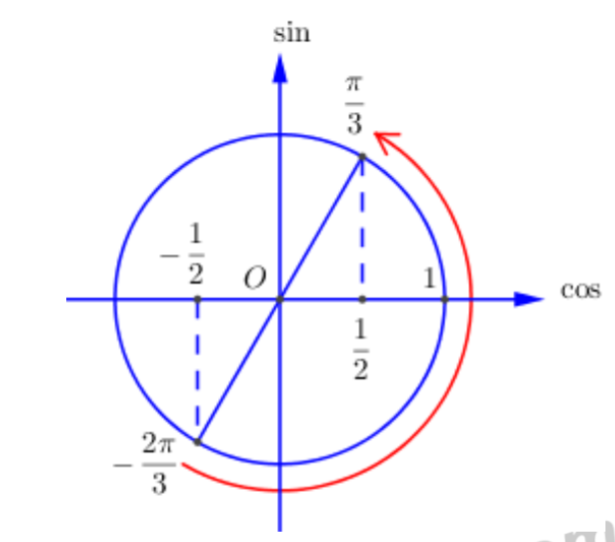
Ta có\[x \in \left[ { - \frac{\pi }{3};\frac{\pi }{6}} \right] \Rightarrow 2x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right].\]

Biểu diễn trên đường tròn lượng giác:

Dựa vào đường tròn lượng giác ta thấy với\[2x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right] \Rightarrow \cos 2x \in \left[ { - \frac{1}{2};1} \right].\]

Vậy\[M = 1;m = - \frac{1}{2} \Rightarrow T = M - 2m = 1 - 2.\left( { - \frac{1}{2}} \right) = 2.\]

Chú ý: Cần biểu diễn trên đường tròn lượng giác, nhiều học sinh nhầm lẫn\[2x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right] \Rightarrow \cos 2x \in \left[ { - \frac{1}{2};\frac{1}{2}} \right].\]

Câu 5

Tìm tập xác định của hàm số\[y = \tan x.\]
A. \[\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi \left. {} \right|k \in \mathbb{Z}} \right\}\]
B. \[\mathbb{R}\backslash \left\{ {k\pi \left. {} \right|k \in \mathbb{Z}} \right\}\]
C. \[\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi \left. {} \right|k \in \mathbb{Z}} \right\}\]
D. \[\mathbb{R}\backslash \left\{ {k2\pi \left. {} \right|k \in \mathbb{Z}} \right\}\]

Lời giải

Đáp án A

Phương pháp:

Hàm số \[y = \tan x\]xác định\[ \Leftrightarrow \cos x \ne 0.\]

Cách giải:

Hàm số \[y = \tan x\]xác định\[ \Leftrightarrow \cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right).\]

Vậy tập xác định\[\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi \left. {} \right|k \in \mathbb{Z}} \right\}.\]

Câu 6

Cho ba điểm\[A\left( {1;2} \right),B\left( {2;3} \right),C\left( {6;7} \right)\]. Giả sử qua phép tịnh tiến theo vectơ \[\overrightarrow u \]các điểm A, B, C lần lượt biến thành các điểm\[A'\left( {2;0} \right),B',C'\]. Khẳng định nào sau đây là đúng?
A. \[B'\left( {3;5} \right)\]
B. \[C'\left( {7;5} \right)\]
C. \[\overrightarrow u \left( {3;2} \right)\]
D. \[\overrightarrow u \left( {1;2} \right)\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Gieo con súc sắc cân đối đồng chất 2 lần. Tính xác suất để tích số chấm xuất hiện ở hai lần là một số tự nhiên lẻ?
A. \[\frac{3}{4}\]
B. \[\frac{1}{4}\]
C. \[\frac{1}{2}\]
D. \[\frac{1}{6}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Tập nghiệm của phương trình \[\cos x = \frac{{\sqrt 2 }}{2}\]là:
A. \[\left\{ {\frac{{3\pi }}{4} + k2\pi ,k \in \mathbb{Z}} \right\}\]
B. \[\left\{ { - \frac{\pi }{4} + k2\pi ,\frac{{5\pi }}{4} + k2\pi \,\,k \in \mathbb{Z}} \right\}\]
C. \[\left\{ { \pm \frac{{3\pi }}{4} + k2\pi ,k \in \mathbb{Z}} \right\}\]
D. \[\left\{ { \pm \frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}} \right\}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Tìm tập xác định của hàm số\[y = \sqrt {\frac{{1 + \cos x}}{{1 - \sin x}}} .\]
A. \[\mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\]
B. \[\mathbb{R\backslash \left\{ {\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\] 
C. \[\mathbb{R}\]
D. \[\mathbb{R}\backslash \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm cạnh SC. Xét các mệnh đề:

 (I)  . Đường thẳng IO song song SA.

 (II) . Mặt phẳng (IBD) cắt hình chóp S.ABCD theo thiết diện là một tứ giác.

 (III)  . Giao điểm của đường thẳng AI và mặt phẳng (SBD) là trọng tâm tam giác SBD.

 (IV)  . Giao tuyến hai mặt phẳng (IBD) và (SAC) là OI.

Số mệnh đề đúng trong các mệnh đề trên là:
A. 4
B. 2
C. 3
D. 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Tìm số hạng không chứa x trong khai triển\[{\left( {{x^3} - \frac{1}{x}} \right)^{12}}.\]
A. – 220
B. 220
C. 924
D. – 924

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Trong các hàm số sau, hàm số nào là hàm số chẵn trên\[\mathbb{R}\]?
A. \[y = \sin \left( {\frac{\pi }{2} - x} \right)\]
B. \[y = \tan x\]
C. \[y = \sin x\]
D. \[y = \sin \left( {x + \frac{\pi }{6}} \right)\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Trong mặt phẳng tọa độ Oxy cho đường tròn\[\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4\]. Phép đối xứng trục Ox biến đường tròn (C) thành đường tròn\[\left( {C'} \right)\]có phương trình là:
A. \[{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4\]
B. \[{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4\]
C. \[{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 4\]
D. \[{\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 4\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. Trên cạnh BD lấy điểm K sao cho BK = 2KD. Gọi F là giao điểm của AD với mặt phẳng (IJK). Tính tỉ số\[\frac{{FA}}{{FD}}.\]
A. \[\frac{7}{3}\]
B. 2
C. \[\frac{{11}}{5}\]
D. \[\frac{5}{3}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Hình nào sau đây có vô số tâm đối xứng?
A. Hình vuông.
B. Hình tròn
C. Đường thẳng
D. Đoạn thẳng

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Hàm số nào sau đây đồng biến trên khoảng\[\left( {\frac{\pi }{2};\pi } \right)\]?
A. \[y = \cos x\]
B. \[y = \tan x\]
C. \[y = \cot x\]
D. \[y = \sin x\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Cho hai đường thẳng song song. Trên đường thẳng thứ nhất ta lấy 20 điểm phân biệt. Trên đường thẳng thứ hai ta lấy 18 điểm phân biệt. Hỏi có bao nhiêu tam giác được tạo thành từ 3 điểm trong các điểm nói trên?
A. \[18C_{20}^2 + 20C_{18}^2\]
B. \[20C_{18}^3 + 18C_{20}^3\]
C. \[C_{38}^3\]
D. \[C_{20}^3C_{18}^3\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Xét phép vị tự tâm I với tỉ số k = 3 biến\[\Delta ABC\]thành\[\Delta A'B'C'\]. Hỏi diện tích\[\Delta A'B'C'\]gấp mấy lần diện tích\[\Delta ABC\]?
A. 6
B. 27
C. 3
D. 9

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Số nghiệm của phương trình\[\left( {2x - \frac{{5\pi }}{6}} \right) + \sqrt 3 = 0\]trên khoảng \[\left( {0;3\pi } \right).\]
A. 6
B. 27
C. 3
D. 9

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Tính tổng T các nghiệm của phương trình \[{\cos ^2}x = \sin x\cos x + 2\sin x - \cos x - 2\]trên khoảng\[\left( {\frac{\pi }{2};5\pi } \right).\]
A. \[T = \frac{{15\pi }}{2}\]
B. \[T = \frac{{21\pi }}{8}\]
C. \[T = 7\pi \]
D. \[T = \frac{{3\pi }}{4}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Cho phương trình\[\cos 2\left( {x + \frac{\pi }{3}} \right) + 20\cos \left( {\frac{\pi }{6} - x} \right) + 11 = 0\]. Khi đặt\[t = \cos \left( {\frac{\pi }{6} - x} \right)\], phương trình đã cho trở thành phương trình nào dưới đây?
A. \[{t^2} + 20t + 12 = 0\]
B. \[{t^2} - 20t + 11 = 0\]
C. \[ - {t^2} + 10t + 6 = 0\]
D. \[{t^2} + 10t + 5 = 0\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Tính số các chỉnh hợp chập 4 của 7 phần tử:
A. 720
B. 35
C. 840
D. 24

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Xét đường tròn lượng giác như hình vẽ, biết\[BOC = BOF = 30^\circ \]lần lượt là các điểm đối xứng với C, F qua gốc O. Nghiệm của phương trình\[2\sin x - 1 = 0\]được biểu diễn trên đường tròn lượng giác là những điểm nào?
A. Điểm C, điểm D
B. Điểm E, điểm F
C. Điểm C, điểm F
D. Điểm E, điểm D

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

Biết hệ số của số hạng chứa\[{x^2}\]trong khai triển\[{\left( {1 + 4x} \right)^n}\]là 3040. Số tự nhiên n bằng bao nhiêu?
A. 24
B. 26
C. 28
D. 20

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

Một bộ đề thi Olimpic Toán lớp 11 của Trường THPT Kim Liên mà mỗi đề gồm 5 câu được chọn từ 15 câu mức dễ, 10 câu mức trung bình và 5 câu mức khó. Một đề thi được gọi là “Tốt” nếu trong đề thi phải có cả mức dễ, trung bình và khó, đồng thời số câu mức khó không ít hơn 2. Lấy ngẫu nhiên một đề thi trong bộ đề trên. Tìm xác suất để đề thi lấy ra là một đề thi “Tốt”.
A. \[\frac{{1000}}{{5481}}\]
B. \[\frac{1}{{150}}\]
C. \[\frac{{10}}{{71253}}\]
D. \[\frac{{3125}}{{23751}}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

a)  Giải phương trình\[{\cos ^2}x + \sin 2x - 3{\sin ^2}x = - 2.\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

b)  Một hộp đựng tám thẻ được ghi từ 1 đến 8. Lấy ngẫu nhiên từ hộp đó ba thẻ, tính xác suất để tổng các số ghi trên ba thẻ đó bằng 11.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có phương trình\[{x^2} + {y^2} - 2x + 4y - 4 = 0\]và điểm I (2;l). Phép vị tự tâm I tỉ số k = 2 biến đường tròn\[\left( C \right)\]thành đường tròn (C'). Viết phương trình đường tròn\[\left( {C'} \right)\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

Cho n là số nguyên dương chẵn bất kì, chứng minh

\[\frac{1}{{1!\left( {n - 1} \right)!}} + \frac{1}{{3!\left( {n - 3} \right)!}} + \frac{1}{{5!\left( {n - 5} \right)!}} + ... + \frac{1}{{\left( {n - 1} \right)!1!}} = \frac{{{2^{n - 1}}}}{{n!}}\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, I lần lượt là trung điểm của SA, SB, BC; điểm G nằm giữa S và I sao cho\[\frac{{SG}}{{SI}} = \frac{3}{5}\].

a)  Tìm giao điểm của đường thẳng MG và mặt phẳng (ABCD).

b) Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (MNG).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập

Đăng ký

Bạn đã có tài khoản?