Bộ 20 đề thi học kì 1 Toán 11 năm 2022

Thi Online Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án

Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 5)

4343 lượt thi
24 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Trong mặt phẳng Oxy, cho đường thẳng \(\Delta :2{\rm{x}} - 3y - 5 = 0\). Ảnh của đường Δ qua phép tịnh tiến theo vectơ \(\overrightarrow u = \left( { - 1;2} \right)\) là đường thẳng nào?

A. \(2{\rm{x}} - 3y + 13 = 0\)

B. \(2{\rm{x}} - 3y - 3 = 0\)

C. \(2{\rm{x}} - 3y - 13 = 0\)

D. \(2{\rm{x}} - 3y + 3 = 0\)

Xem đáp án

Đáp án D

Phương pháp:

Sử dụng định nghĩa về phép tịnh tiến trong mặt phẳng.

Cách giải:

Gọi \(M\left( {x;y} \right) \in \Delta ;{\rm{ }}{{\rm{T}}_{\overrightarrow n }}\left( M \right) = M'\left( {x';y'} \right) \in \Delta '\)

\( \Rightarrow \left\{ \begin{array}{l}x' = x - 1\\y' = y + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = x' + 1\\y = y' - 2\end{array} \right. \Rightarrow M\left( {x' + 1;y' - 2} \right) \in {\rm{d}}\)

\(M \in d \Rightarrow 2\left( {x' + 1} \right) - 3\left( {y' - 2} \right) - 5 = 0 \Leftrightarrow 2{\rm{x'}} - 3y' + 3 = 0\)

Vậy phương trình ảnh của đường thẳng Δ là: \(\Delta ' = 2{\rm{x}} - 3y + 3 = 0\).

Câu 2:

Từ các chữ số của tập \(X = \left\{ {1;2;4;5;7;8} \right\}\) có thể lập được bao nhiêu số tự nhiên có bốn chữ số đôi một khác nhau?

A. \({4^6}\)

B. \(A_6^4\)

C. \(C_6^4\)

D. \({6^4}\)

Xem đáp án

Đáp án B

Phương pháp:

Sử dụng định nghĩa chỉnh hợp.

Cách giải:

Số cách lấy các số tự nhiên có bốn chữ số khác nhau từ tập X gồm 6 phần tử là: \(A_6^4\).

Câu 3:

Hệ số của số hạng thứ 6 trong khai triển biểu thức \({\left( {2{{\rm{x}}^3} + y} \right)^{10}}\) bằng?

A. 8064

B. \(3360{{\rm{x}}^4}{y^6}\)

C. 3360

D. \(8064{{\rm{x}}^{10}}{y^5}\)

Xem đáp án

Đáp án A

Phương pháp:

Khai triển biểu thức, số hạng thứ 6 ứng với \(k = 5\) rồi tìm hệ số.

Cách giải:

Ta có: \({\left( {2{{\rm{x}}^2} + y} \right)^{10}} = \sum\limits_{k = 0}^{10} {C_{10}^k{{\left( {2{{\rm{x}}^2}} \right)}^{10 - k}}{y^k}} \). Số hạng thứ 6 ứng với \(k = 5\)

\( \Rightarrow C_{10}^5{\left( {2{{\rm{x}}^2}} \right)^{10 - 5}}{y^5} = {2^5}C_{10}^5{x^{10}}{y^5} = 8064{{\rm{x}}^{10}}{y^5}\). Hệ số là: 8064.

Câu 4:

Số nghiệm của phương trình \(\cos 2x = \frac{1}{2}\) trên nửa khoảng \(\left( {0^\circ ;360^\circ } \right]\) là?

A. 8

B. 6

C. 2

D. 4

Xem đáp án

Đáp án D

Phương pháp:

Giải phương trình tìm nghiệm, kẹp nghiệm trong nửa khoảng đã cho tìm số nghiệm thỏa mãn.

Cách giải:

Ta có: \(\cos 2x = \frac{1}{2} \Leftrightarrow \cos 2x = \cos \frac{\pi }{3} \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{3} + k2\pi \\2x = - \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow x = \pm \frac{\pi }{6} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).

Trên nửa khoảng \(\left( {0^\circ ;360^\circ } \right]\) tức \(\left( {0;2\pi } \right]\). Ta sẽ có các nghiệm thỏa mãn như sau:

+) \(0 < x = \frac{\pi }{6} + k\pi \le 2\pi \Leftrightarrow - \frac{1}{6} < k \le \frac{{11}}{6}\) mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ {0;1} \right\}\). Có 2 nghiệm.

+) \(0 < x = - \frac{\pi }{6} + k\pi \le 2\pi \Leftrightarrow \frac{1}{6} < k \le \frac{{13}}{6}\) mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ {1;2} \right\}\). Có 2 nghiệm.

Vậy có 4 nghiệm thỏa mãn yêu cầu bài toán.

Câu 5:

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. G là trung điểm của MN, I là giao điểm của đường thẳng AG và mặt phẳng \(\left( {BC{\rm{D}}} \right)\). Tính tỉ số \(\frac{{GI}}{{GA}}\)?

A. \[\frac{{GI}}{{GA}} = \frac{1}{4}\]

B. \[\frac{{GI}}{{GA}} = \frac{1}{5}\]

C. \[\frac{{GI}}{{GA}} = \frac{1}{2}\]

D. \[\frac{{GI}}{{GA}} = \frac{1}{3}\]

Xem đáp án

Đáp án D

Phương pháp:

Vẽ hình sau đó sử dụng định lý Ta-lét trong tam giác.

Cách giải:

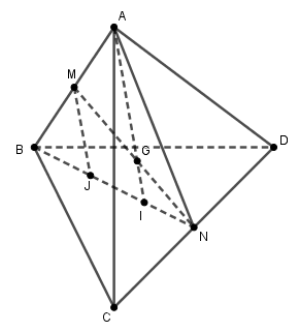
Trong \(\left( {ABN} \right)\) qua M kẻ đường thẳng song song với AI cắt BN tại J.

Xét tam giác MNJ ta có: \(\left\{ \begin{array}{l}GI{\rm{ // MJ}}\\{\rm{GN}} = GM\left( {gt} \right)\end{array} \right. \Rightarrow GI = \frac{1}{2}MJ\) (1).

Xét tam giác BAI ta có: \(\left\{ \begin{array}{l}{\rm{MJ // AI}}\\{\rm{MA}} = MB\end{array} \right. \Rightarrow MJ = \frac{1}{2}AI\) (2).

Từ (1) và (2) \( \Rightarrow GI = \frac{1}{4}AI \Leftrightarrow \frac{{GI}}{{GA}} = \frac{1}{3}\).

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Bài thi liên quan:

Các bài thi hot trong chương:

Đề thi Toán lớp 11 Học kì 1 có đáp án

( 8.2 K lượt thi )

Đề thi Toán 11 Học kì 1 có đáp án

( 5.2 K lượt thi )

Đề kiểm tra giữa học kì 1 Toán lớp 11 có đáp án (Mới nhất)

( 4.2 K lượt thi )

Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án

( 3.9 K lượt thi )

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

( 8.5 K lượt thi )

Top 4 Đề thi Toán 11 Học kì 2 có đáp án

( 8 K lượt thi )

Đề thi Toán 11 Học kì 2 có đáp án

( 5.6 K lượt thi )

Đánh giá trung bình

Thi Online Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án