Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 12)

Phương pháp

1)    Sử dụng công thức nhân đôi đưa phương trình về phương trình bậc hai với ẩn \[\cos x\].

2)    Sử dụng công thức cộng \[\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\] và biến đổi phương trình về dạng tích.

Cách giải

1.

Vậy phương trình có nghiệm \[x = k\pi ,k \in \mathbb{Z}\].

2.

\[\begin{array}{l}\cos 3x + \cos x - \cos 2x = 0\\ \Leftrightarrow 2\cos 2x\cos x - \cos 2x = 0 \Leftrightarrow \cos 2x\left( {2\cos x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\cos 2x = 0\\2\cos x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\cos 2x = 0\\\cos x = \frac{1}{2}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{2} + k\pi \\x = \pm \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + \frac{{k\pi }}{2}\\x = \pm \frac{\pi }{3} + k2\pi \end{array} \right.,k \in \mathbb{Z}\end{array}\]

Vậy phương trình có nghiệm \[x = \frac{\pi }{4} + \frac{{k\pi }}{2},x = \pm \frac{\pi }{3} + k2\pi \].

Phương pháp

1)    Sử dụng công thức tính số hạng tổng quát \[{T_{k + 1}} = C_n^k{a^{n - k}}{b^k}\].

2)    Sử dụng khai triển \[{\left( {a + b} \right)^n}\] và chọn a, b, n là các số thích hợp, từ đó quy ra tổng.

Cách giải

1) Tìm số hạng không chứa x trong khai triển của \[{\left( {2{x^3} - \frac{1}{x}} \right)^{12}},x \ne 0\].

Ta có: \[{T_{k + 1}} = C_{12}^k{\left( {2{x^3}} \right)^{12 - k}}.{\left( { - \frac{1}{x}} \right)^k} = C_{12}^k{.2^{12 - k}}.{x^{3\left( {12 - k} \right)}}.\frac{{{{\left( { - 1} \right)}^k}}}{{{x^k}}} = C_{12}^k.{\left( { - 1} \right)^k}{.2^{12 - k}}.{x^{36 - 3k - k}} = C_{12}^k.{\left( { - 1} \right)^k}{.2^{12 - k}}.{x^{36 - 4k}}\].

Số hạng không chứa x nếu \[36 - 4k = 0 \Leftrightarrow k = 9\].

Vậy số hạng không chứa x là \[C_{12}^9.{\left( { - 1} \right)^9}{.2^{12 - 9}} = - 1760\].

2) Chứng minh rằng \[{7^{17}}C_{17}^0 + {3.7^{16}}C_{17}^1 + {3^2}{.7^{15}}.C_{17}^2 + ... + {3^{16}}.7C_{17}^{16} + {3^{17}}C_{17}^{17} = {10^{17}}\].

Số hạng tổng quát \[C_{17}^k{.7^{17 - k}}{.3^k}\], chọn \[n = 17,a = 7,b = 3\].

Xét tổng: \[{\left( {7 + 3} \right)^{17}} = C_{17}^0{.7^{17 - 0}}{.3^0} + C_{17}^1{.7^{17 - 1}}{.3^1} + ... + C_{17}^{16}{.7^{17 - 16}}{.3^{16}} + C_{17}^{17}{.7^0}{.3^{17}}\].

Do đó \[{10^{17}} = {7^{17}}C_{17}^0 + {3.7^{16}}C_{17}^1 + ... + {3^{16}}.7C_{17}^{16} + {3^{17}}C_{17}^{17}\] (đpcm).

Phương pháp

1)    Tính số phần tử không gian mẫu.

Tính số khả năng có lợi cho biến cố.

Sử dụng công thức tính xác suất \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\].

2)    Sử dụng các quy tắc nhân xác suất, xác suất biến cố đối.

Cách giải

1) Một hộp chứa 3 quả cầu đen và 2 quả cầu trắng. Lấy ngẫu nhiên đồng thời 2 quả. Tính xác suất để lấy được hai quả cầu khác màu.

Phép thử: “Lấy ngẫu nhiên 2 quả cầu”.

\[ \Rightarrow n\left( \Omega \right) = C_5^2 = 10\].

Biến cố A: “Chọn được hai quả cầu khác màu”.

\[ \Rightarrow n\left( A \right) = C_3^1.C_2^1 = 3.2 = 6\].

Xác suất \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{6}{{10}} = \frac{3}{5}\].

2) Hai người tham gia một trò chơi ném bóng vào rổ, mỗi người ném vào rổ của mình 1 quả bóng. Biết rằng xác suất ném bóng trúng rổ của người thứ nhất, người thứ hai lần lượt là \[\frac{1}{5}\] và \[\frac{2}{7}\] và hai người ném một cách độc lập với nhau.

Gọi \[{B_1}\]: “Người 1 trúng rổ”, \[P\left( {{B_1}} \right) = \frac{1}{5}\].

\[{B_2}\]: “Người 2 trúng rổ”, \[P\left( {{B_2}} \right) = \frac{2}{7}\].

a) Tính xác suất để hai người cùng ném bóng trúng rổ.

Gọi biến cố B: Hai người trúng rổ.

Theo quy tắc nhân xác suất ta có: \[P\left( B \right) = P\left( {{B_1}} \right).P\left( {{B_2}} \right) = \frac{1}{5}.\frac{2}{7} = \frac{2}{{35}}\].

b) Tính xác suất để có ít nhất một người ném không trúng rổ.

Gọi biến cố C: Ít nhất một người không trúng rổ.

Biến cố đối \[\overline C \]: Cả hai người đều trúng rổ.

Dễ thấy đây cũng là biến cố B nên \[P\left( {\overline C } \right) = P\left( B \right) = \frac{2}{{35}}\].

Vậy \[P\left( C \right) = 1 - P\left( {\overline C } \right) = 1 - \frac{2}{{35}} = \frac{{33}}{{35}}\].

Phương pháp

a) - Sử dụng định lý: \[\left\{ \begin{array}{l}a \subset \left( P \right)\\b \subset \left( Q \right)\\a//b\\\left( P \right) \cap \left( Q \right) = d\end{array} \right. \Rightarrow d//a//b\].

- Sử dụng định lý: \[\left\{ \begin{array}{l}a \not\subset \left( P \right)\\a//b\\b \subset \left( P \right)\end{array} \right. \Rightarrow a//\left( P \right)\].

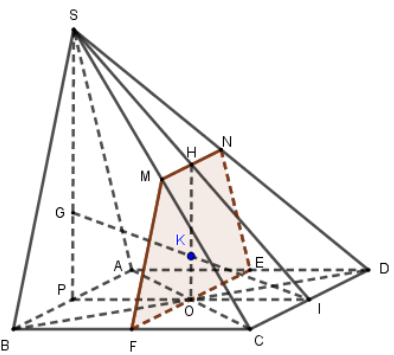
Cách giải

1) Tìm giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\]. Chứng minh rằng đường thẳng MN song song với mặt phẳng \[\left( {SAB} \right)\].

+ Ta có: \[\left\{ \begin{array}{l}AB \subset \left( {SAB} \right)\\CD \subset \left( {SCD} \right)\\AB//CD\\\left( {SAB} \right) \cap \left( {SCD} \right) = Sx\end{array} \right. \Rightarrow Sx//AB//CD\].

Do đó giao tuyến của \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\] là đường thẳng Sx đi qua S và song song với AB, CD.

+ Dễ thấy \[MN \not\subset \left( {SAB} \right)\]

Trong tam giác SCD có M, N là trung điểm SC, SD nên MN là đường trung bình của tam giác SCD.

Khi đó \[MN//CD\], mà \[CD//AB\] nên \[MN//AB\].

Mà \[AB \subset \left( {SAB} \right)\] nên \[MN//\left( {SAB} \right)\] (đpcm).

Phương pháp