Bộ 20 đề thi học kì 1 Toán 11 năm 2022

Thi Online Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án

Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 4)

4332 lượt thi
23 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Trong không gian cho 10 điểm phân biệt, trong đó không có 4 điểm nào đồng phẳng. Số các hình tứ diện có thể kẻ được là:

A. 210.

B. 105.

C. 315.

D. 420.

Xem đáp án

Đáp án A

Phương pháp:

- Tứ diện là hình có 4 đỉnh không đồng phẳng.

- Sử dụng tổ hợp.

Cách giải:

Chọn 4 điểm từ 10 điểm ta được 1 hình tứ diện.

Vậy số tứ diện có thể kẻ được là \(C_{10}^4 = 210\).

Câu 2:

Hệ số của \[{x^{12}}\]trong khai triển \[{\left( {{x^2} + x} \right)^{10}}\] là

A. \(C_{10}^6{.2^6}\).

B. \(C_{10}^6\).

C. \(C_{10}^8\).

D. \( - C_{10}^2\).

Xem đáp án

Đáp án C

Phương pháp:

- Sử dụng khai triển nhị thức Newton: \[{\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \].

- Sử dụng công thức \[C_n^k = C_n^{n = k}\].

Cách giải:

Ta có: \[{\left( {{x^2} + x} \right)^{10}} = \sum\limits_{k = 0}^{10} {C_{10}^k{{\left( {{x^2}} \right)}^k}.{x^{10 - k}}} = \sum\limits_{k = 0}^{10} {C_{10}^k.{x^{10 + k}}{\rm{ }}} \left( {0 \le k \le 10;{\rm{ }}k \in \mathbb{N}} \right)\].

Số hạng chứa \[{x^{12}}\] ứng với \[10 + k = 2 \Leftrightarrow k = 2\left( {tm} \right)\].

Vậy hệ số của \[{x^{12}}\] trong khai triển trên là \[C{\kern 1pt} _{10}^2 = C_{10}^8\].

Câu 3:

Cho hình chóp \(S.ABCD\). Gọi \(M\)và \(N\) lần lượt là trung điểm của \(SA\) và \(SC\). Khẳng định nào sau đây là đúng?

A. \(MN||mp\left( {ABCD} \right)\).

B. \(MN||mp\left( {SAB} \right)\).

C. \(MN||mp\left( {SBC} \right)\).

D. \(MN||mp\left( {SCD} \right)\).

Xem đáp án

Đáp án A

Phương pháp:

\[\left\{ \begin{array}{l}a||b\\b \subset \left( P \right)\end{array} \right. \Rightarrow a||\left( P \right)\]

Cách giải:

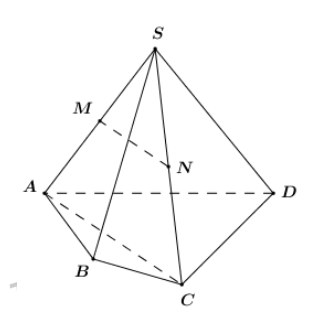
Vì \(MN\) là đường trung bình của tam giác \(SAC\).

\( \Rightarrow MN||AC\) (Tính chất đường trung bình).

Mà \[AC \subset \left( {ABCD} \right) \Rightarrow MN||\left( {ABCD} \right)\].

Câu 4:

Trong mặt phẳng tọa độ Oxy, cho \(\Delta :x - 2y - 1 = 0\) và \(\overrightarrow u \left( {4;3} \right)\). Gọi \(d\) là đường thẳng sao cho \({T_{\overrightarrow u }}\) biến \(d\) thành đường thẳng \(\Delta \). Phương trình đường thẳng \(d\) là

A. \(x - 2y + 1 = 0\).

B. \(x - 2y + 9 = 0\).

C. \(x - 2y - 3 = 0\).

D. \(x - 2y - 9 = 0\).

Xem đáp án

Đáp án A

Phương pháp:

Phép tính tiến biến đường thẳng thành đường thẳng song song với nó.

Cách giải:

Vì \(\Delta = {T_{\overrightarrow u }}\left( d \right) \Rightarrow \Delta ||d\) Þ Phương trình \(\Delta \) có dạng: \(x - 2y + c = 0\left( \Delta \right)\).

Lấy \(A\left( {1;0} \right)\) bất kì thuộc \(d\). Gọi \(A' = {T_{\overrightarrow u }}\left( A \right) \Rightarrow A' \in \Delta \).

Ta có: \(A' \in {T_{\overrightarrow u }}\left( A \right) \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = {x_A} + {x_{\overrightarrow u }} = 1 + 4 = 5\\{y_{A'}} = {y_A} + {y_{\overrightarrow u }} = 0 + 3 = 3\end{array} \right. \Rightarrow A'\left( {5;3} \right)\).

Vì \(A' \in \Delta \Rightarrow 5 - 2.3 + c = 0 \Leftrightarrow c = 1\).

Vậy phương trình đường thẳng \(\Delta \) là: \(x - 2y + 1 = 0\).

Câu 5:

Cho hình vuông ABCD tâm O. Ảnh của đường thẳng CD qua phép quay tâm O, góc quay -90° là:

A. đường thẳng AB.

B. đường thẳng AC.

C. đường thẳng DA.

D. đường thẳng BC.

Xem đáp án

Đáp án C

Phương pháp:

Vẽ hình và xác định ảnh của hai điểm \(C,\,\,D\) qua phép quay tâm \(O\), góc quay \( - 90^\circ \).

Cách giải:

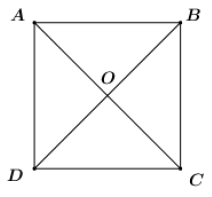
Vì \(ABCD\) là hình vuông nên \(OA = OB = OC = OD\) và \(AC \bot BD\) tại \(O\).

Khi đó ta có: \({Q_{\left( {O; - 90^\circ } \right)}}\left( C \right) = D,{\rm{ }}{Q_{\left( {O; - 90^\circ } \right)}}\left( D \right) = A\).

Vậy \({Q_{\left( {O; - 90^\circ } \right)}}\left( {CD} \right) = DA\).

Chú ý: Phép quay góc có giá trị âm là phép quay cùng chiều kim đồng hồ.

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Bài thi liên quan:

Các bài thi hot trong chương:

Đề thi Toán lớp 11 Học kì 1 có đáp án

( 8.2 K lượt thi )

Đề thi Toán 11 Học kì 1 có đáp án

( 5.2 K lượt thi )

Đề kiểm tra giữa học kì 1 Toán lớp 11 có đáp án (Mới nhất)

( 4.2 K lượt thi )

Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án

( 3.9 K lượt thi )

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

( 8.5 K lượt thi )

Top 4 Đề thi Toán 11 Học kì 2 có đáp án

( 8 K lượt thi )

Đề thi Toán 11 Học kì 2 có đáp án

( 5.6 K lượt thi )

Đánh giá trung bình

Thi Online Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án