Bộ 20 đề thi học kì 1 Toán 11 năm 2022

Thi Online Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án

Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 19)

1713 lượt thi
22 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Tập xác định của hàm số \[y = \frac{{\sin {\mkern 1mu} x + \cos x}}{{\tan {\mkern 1mu} x}}\] là:

A. \[R\backslash \left\{ {k\pi ,k \in Z} \right\}\]

B. \[R\backslash \left\{ { - \frac{\pi }{4} + k\pi ,k \in Z} \right\}\]

C. \[R\backslash \left\{ {k\frac{\pi }{2},k \in Z} \right\}\]

D. \[R\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in Z} \right\}\]

Xem đáp án

Đáp án C

Phương pháp giải:

Hàm phân thức xác định khi mẫu thức khác 0.

Hàm \[\tan x\] xác định \[ \Leftrightarrow \sin x \ne 0\].

Giải chi tiết:

ĐKXĐ: \[\left\{ {\begin{array}{*{20}{l}}{\tan {\mkern 1mu} x \ne 0}\\{\cos x \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\sin x \ne 0}\\{\cos x \ne 0}\end{array}} \right. \Leftrightarrow \sin 2x \ne 0 \Leftrightarrow 2x \ne k\pi \Leftrightarrow x \ne k\frac{\pi }{2}{\mkern 1mu} {\mkern 1mu} \left( {k \in Z} \right)\]

TXĐ: \[D = R\backslash \left\{ {k\frac{\pi }{2},k \in Z} \right\}\].

Câu 2:

Phương trình \[{\sin ^2}x = 1\] tương đương với phương trình nào sau đây?

A. \[\sin x = 1\]

B. \[\cos x = - 1\]

C. \[\cos 2x = 1\]

D. \[\cos 2x = - 1\]

Xem đáp án

Đáp án D

Phương pháp giải:

Sử dụng công thức nhân đôi: \[\cos 2x = 1 - 2{\sin ^2}x\]

Giải chi tiết:

Ta có: \[{\sin ^2}x = 1 \Leftrightarrow \cos 2x = 1 - 2{\sin ^2}x = 1 - 2.1 = - 1\]

Câu 3:

Trên khoảng \[\left( { - \frac{{3\pi }}{4};\frac{\pi }{4}} \right)\] tập giá trị của hàm số \[y = \cos x\] là:

A. \[\left( { - \frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right)\]

B. \[\left( { - \frac{{\sqrt 2 }}{2};1} \right)\]

C. \[\left[ { - \frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right]\]

D. \[\left( { - \frac{{\sqrt 2 }}{2};1} \right]\]

Xem đáp án

Đáp án D

Phương pháp giải:

Biểu diễn các góc lượng giác thuộc khoảng \[\left( { - \frac{{3\pi }}{4};\frac{\pi }{4}} \right)\] trên đường tròn lượng giác, từ đó kết luận tập giá trị của hàm số \[y = \cos x\] trên khoảng đó.

Giải chi tiết:

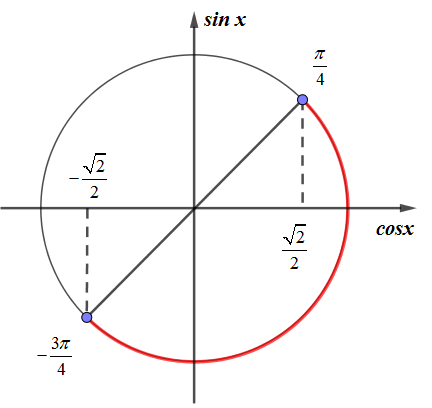
Biểu diễn các góc lượng giác thuộc khoảng \[\left( { - \frac{{3\pi }}{4};\frac{\pi }{4}} \right)\] trên đường tròn lượng giác, ta thấy: tập giá trị của hàm số \[y = \cos x\] trên khoảng đó là: \[\left( { - \frac{{\sqrt 2 }}{2};1} \right]\]

Câu 4:

Cho phương trình \[\sin 2x + \sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right) = 1\]. Đặt \[t = \sin {\mkern 1mu} x - \cos x\] ta được phương trình nào sau đây?

A. \[{t^2} + t = 0\]

B. \[{t^2} + 2t - 1 = 0\]

C. \[{t^2} + 2t - 1 = 0\]

D. \[{t^2} - t = 0\]

Xem đáp án

Đáp án D

Phương pháp giải:

\[\sin 2x = 2\sin {\mkern 1mu} x\cos x;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right) = \sin x - \cos x\]

Giải chi tiết:

Ta có: \[\sin 2x + \sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right) = 1 \Leftrightarrow 2\sin x\cos x + \left( {\sin {\mkern 1mu} x - \cos x} \right) = 1\] (1)

Đặt \[t = \sin {\mkern 1mu} x - \cos x \Leftrightarrow {t^2} = {\left( {\sin {\mkern 1mu} x - \cos x} \right)^2} \Leftrightarrow {t^2} = 1 - 2\sin x\cos x \Leftrightarrow 2\sin x\cos x = 1 - {t^2}\]

Khi đó, \[\left( 1 \right) \Leftrightarrow 1 - {t^2} + t = 1 \Leftrightarrow {t^2} - t = 0\]

Câu 5:

Gọi S là tập hợp tất cả các số thực m để phương trình \[4{\cos ^3}x + 2\cos 2x + 2 = \left( {m + 3} \right)\cos x\] có đúng 5 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\]. Kết luận nào sau đây đúng?

A. \[S \subset \left( {0;7} \right)\]

B. \[\left( { - 2;8} \right) \subset S\]

C. \[S \cap \left( {0; + \infty } \right) = \emptyset \]

D. \[S \subset \left( { - 3;5} \right)\]

Xem đáp án

Đáp án D

Phương pháp giải:

Giải chi tiết:

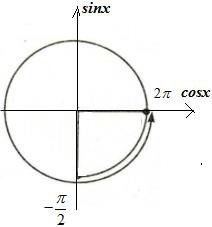
Ta có:

\[{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} 4{\cos ^3}x + 2\cos 2x + 2 = \left( {m + 3} \right)\cos x{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (*){\mkern 1mu} \]

\[ \Leftrightarrow 4{\cos ^3}x + 4{\cos ^2}x - \left( {m + 3} \right)\cos x = 0\]

\[ \Leftrightarrow \left( {4{{\cos }^2}x + 2\cos x - \left( {m + 3} \right)} \right).\cos x = 0\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{4{{\cos }^2}x + 4\cos x - \left( {m + 3} \right) = 0{\mkern 1mu} {\mkern 1mu} (1)}\\{\cos x = 0{\mkern 1mu} {\mkern 1mu} (2)}\end{array}} \right.\]

Phương trình \[(2) \Leftrightarrow x = \frac{\pi }{2} + k\pi {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {k \in Z} \right)\]. Mà \[x \in \left( { - \frac{\pi }{2};2\pi } \right] \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2}}\\{x = \frac{{3\pi }}{2}}\end{array}} \right.\]

Thay \[\cos x = 0\] vào (1): \[{4.0^2} + 4.0 - \left( {m + 3} \right) = 0 \Leftrightarrow m = - 3\]

+) Với \[m = - 3\]:

Phương trình \[(1) \Leftrightarrow 4{\cos ^2}x + 4\cos x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\cos x = 0}\\{\cos x = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2} + k\pi }\\{x = \pi + k2\pi }\end{array}} \right.{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} ,k \in \mathbb{Z}\]

Mà \[x \in \left( { - \frac{\pi }{2};2\pi } \right] \Rightarrow x \in \left\{ {\frac{\pi }{2};\frac{{3\pi }}{2};\pi } \right\}\]

Phương trình \[(*)\] có đúng 3 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\] là \[\left\{ {\frac{\pi }{2};\frac{{3\pi }}{2};\pi } \right\} \Rightarrow m = - 3\] không thỏa mãn

+) Với \[m \ne - 3\]: Phương trình (1) không có nghiệm \[x = \frac{\pi }{2},{\mkern 1mu} {\mkern 1mu} x = \frac{{3\pi }}{2}\]. Khi đó, để (*) có đúng 5 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\] thì phương trình (1) có đúng 3 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\]

Đặt \[\cos x = t\], (1) trở thành: \[4{t^2} + 4t - \left( {m + 3} \right) = 0\] (3)

Phương trình (1) có đúng 3 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\]⇔ Phương trình (3) có 2 nghiệm \[{t_1},{\mkern 1mu} {\mkern 1mu} {t_2}{\mkern 1mu} {\mkern 1mu} \left( {{t_1} \le {t_2}} \right)\] thỏa mãn:

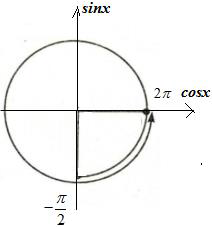
Media VietJack

hoặc \[\left\{ {\begin{array}{*{20}{l}}{{t_1} = - 1}\\{{t_2} \in \left( { - 1;0} \right] \cup \left\{ 1 \right\}}\end{array}} \right.\], hoặc \[{t_1} = {t_2} \in \left( {0;1} \right)\], hoặc \[\left\{ {\begin{array}{*{20}{l}}{{t_1} \in \left( {0;1} \right)}\\{{t_2} > 1}\end{array}} \right.\], hoặc \[\left\{ {\begin{array}{*{20}{l}}{{t_1} < - 1}\\{{t_2} \in \left( {0;1} \right)}\end{array}} \right.\]

TH1: \[\left\{ {\begin{array}{*{20}{l}}{{t_1} = - 1}\\{{t_2} \in \left( { - 1;0} \right] \cup \left\{ 1 \right\}}\end{array}} \right.\]

\[ \Rightarrow 4.{\left( { - 1} \right)^2} + 4.\left( { - 1} \right) - \left( {m + 3} \right) = 0 \Leftrightarrow m = - 3\] (loại)

TH2: \[{t_1} = {t_2} \in \left( {0;1} \right)\]

\[ \Rightarrow \Delta ' = 0 \Leftrightarrow 4 + 4\left( {m + 3} \right) \Leftrightarrow 4m + 16 = 0 \Leftrightarrow m = - 4\]

Khi đó, (3) có 2 nghiệm \[{t_1} = {t_2} = - \frac{1}{2} \notin \left( {0;1} \right){\mkern 1mu} {\mkern 1mu} \Rightarrow m = - 4\]: không thỏa mãn

TH3:

\[\left\{ {\begin{array}{*{20}{l}}{{t_1} \in \left( {0;1} \right)}\\{{t_2} > 1}\end{array}} \right. \Leftrightarrow 0 < {t_1} < 1 < {t_2} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{t_1}{t_2} > 0}\\{{t_1} + {t_2} > 0}\\{\left( {{t_1} - 1} \right)\left( {{t_2} - 1} \right) < 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{t_1}{t_2} > 0}\\{{t_1} + {t_2} > 0}\\{{t_1}{t_2} - \left( {{t_1} + {t_2}} \right) + 1 < 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4m + 16 > 0}\\{ - \frac{{m + 3}}{4} > 0}\\{ - \frac{4}{4} > 0}\\{1 - \left( { - \frac{4}{4}} \right) - \frac{{m + 3}}{4} < 0}\end{array}} \right. \Leftrightarrow m \in \emptyset \]

TH4:

\[\left\{ {\begin{array}{*{20}{l}}{{t_1} < - 1}\\{{t_2} \in \left( {0;1} \right)}\end{array}} \right. \Leftrightarrow {t_1} < - 1 < 0 < {t_2} < 1 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{t_1}{t_2} < 0}\\{\left( {{t_1} + 1} \right)\left( {{t_2} + 1} \right) < 0}\\{\left( {{t_1} - 1} \right) + \left( {{t_2} - 1} \right) < 0}\\{\left( {{t_1} - 1} \right)\left( {{t_2} - 1} \right) > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4m + 16 > 0}\\{ - \frac{{m + 3}}{4} < 0}\\{ - \frac{{m + 3}}{4} + \left( { - \frac{4}{4}} \right) + 1 < 0}\\{ - \frac{4}{4} - 2 < 0}\\{ - \frac{{m + 3}}{4} - \left( { - \frac{4}{4}} \right) + 1 > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m > - 4}\\{m > - 3}\\{m < 5}\end{array}} \right. \Leftrightarrow m \in \left( { - 3;5} \right)\]

Vậy, tập các giá trị thực của m thỏa mãn yêu cầu đề bài là: \[S = \left( { - 3;5} \right)\]

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Bài thi liên quan:

Các bài thi hot trong chương:

Đề thi Toán lớp 11 Học kì 1 có đáp án

( 7.3 K lượt thi )

Đề thi Toán 11 Học kì 1 có đáp án

( 4.1 K lượt thi )

Đề kiểm tra giữa học kì 1 Toán lớp 11 có đáp án (Mới nhất)

( 2.5 K lượt thi )

Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án

( 1.2 K lượt thi )

Top 4 Đề thi Toán 11 Học kì 2 có đáp án

( 6.8 K lượt thi )

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

( 4.7 K lượt thi )

Đề thi Toán 11 Học kì 2 có đáp án

( 4.5 K lượt thi )

Đánh giá trung bình

Thi Online Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án