Có bao nhiêu cách sắp xếp 6 học sinh lớp 11 và 3 học sinh lớp 12 vào một hàng ghế dài gồm 9 ghế sao cho mỗi học sinh lớp 12 ngồi giữa 2 học sinh lớp 11?

Giải chi tiết:

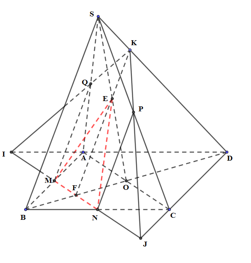
a) Trong (ABCD), gọi \[I = MN \cap AD,\]\[J = MN \cap CD\], \[F = MN \cap BD\]

Trong (SBD), gọi \[K = EF \cap SD\]

Trong (SAD), gọi \[Q = IK \cap SA\]

Trong (SAD), gọi \[P = JK \cap SC\]

Khi đó, thiết diện của hình chóp \[S.ABCD\] cắt bởi mặt phẳng \[\left( {MNE} \right)\] là ngũ giác \[MNPKQ\]

b) MN là đường trung bình của \[\Delta ABC \Rightarrow MN//AC\]

\[ \Rightarrow MF{\rm{//}}AC \Rightarrow \] F là trung điểm của OB \[ \Rightarrow BF = \frac{1}{2}OB = \frac{1}{4}BD \Rightarrow BF = \frac{1}{3}FD\]

Xét \[\Delta SOB\] có: E, F lần lượt là trung điểm của SO, OB \[ \Rightarrow EF\] là đường trung bình của \[\Delta SOB\]

\[ \Rightarrow EF{\rm{//}}SB \Rightarrow FK{\rm{//}}SB \Rightarrow \frac{{KS}}{{KD}} = \frac{{BF}}{{DF}} = \frac{1}{3}\]

Vậy, \[\frac{{KS}}{{KD}} = \frac{1}{3}\]

Đáp án D

Phương pháp giải:

Dựa vào các yếu tố song song xác định thiết diện.

Giải chi tiết:

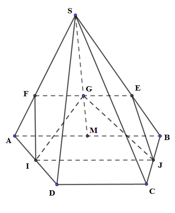
Qua G dựng EF song song AB (\[E \in SB,F \in SA\])

IJ là đường trung bình của hình thang ABCD \[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{IJ{\rm{//}}AB{\rm{//}}CD}\\{IJ = \frac{{AB + CD}}{2}}\end{array}} \right.\]

Ta có: \[\left\{ {\begin{array}{*{20}{l}}{IJ{\rm{//}}AB}\\{AB{\rm{//}}EF}\end{array}} \right. \Rightarrow IJ{\rm{//}}EF \Rightarrow I,J,E,F\] đồng phẳng

\[ \Rightarrow I,J,E,F,G\] đồng phẳng

\[ \Rightarrow \left( {GIJ} \right) \equiv \left( {IJEF} \right)\]

Thiết diện của \[\left( {GIJ} \right)\] với hình chóp là hình thang \[IJEF,{\mkern 1mu} \left( {IJ{\rm{//}}EF} \right)\]

Để thiết diện là hình bình hành thì \[IJ = EF \Leftrightarrow \frac{{AB + CD}}{2} = \frac{2}{3}AB\] (do \[\frac{{EF}}{{AB}} = \frac{{SE}}{{SB}} = \frac{{SG}}{{SM}} = \frac{2}{3}\])

\[ \Leftrightarrow 3AB + 3CD = 4AB \Leftrightarrow AB = 3CD\]